UFES, Cálculo I, Lista 7, 2018.1, questão 15f
Considere as funções
e
(f) Esboce os gráficos de, e
Passo 1
Faaaaala, galeeeera! Como estão, tudo belezinha?
Nessa questão vamos desenhar um gráfico para a função a e a composta entre as duas.
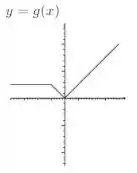
Esboçando a :
Teremos uma linha reta (), quando temos valores negativos de . E teremos quando temos valores maiores ou iguais a zero.
Vamos encontrar as raízes da equação do segundo grau.
Podemos tirar a raiz
Essa função intercepta o eixo quando , em
Então o ponto que a função corta o eixo é . Podemos então esboçar esse gráfico. Como é negativo, a concavidade é voltada para baixo, ok?
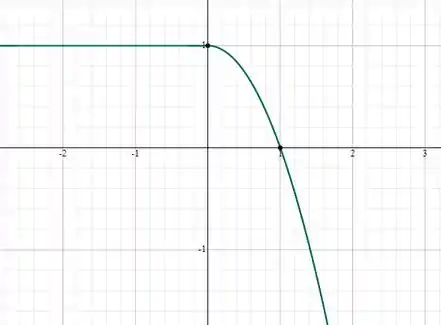
Passo 2
Agora, traçando o gráfico de . Temos que ver que quando nossa função é uma e quando a função de determinar por um módulo. O módulo rebate todos os valores negativos para a parte positiva do gráfico.
Para traçar , basta plotar alguns pontos.
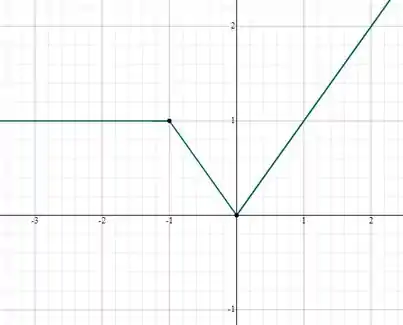
Passo 3
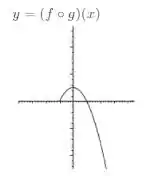
Por fim, para , teremos a para e a mesma função quadrática da para.
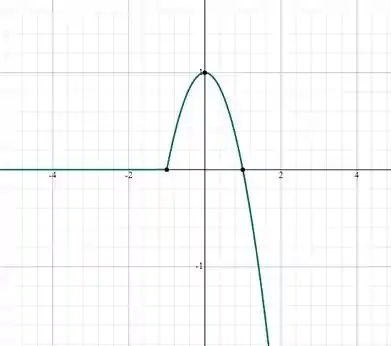
Prontinho! Até mais!
Resposta
