Verifique se existem as funções compostas e quando e são definidas tais como nos itens a seguir. Caso exista a composição, explicite qual é o seu domínio e contradomínio e, em seguida, determine a sua lei.
tal que
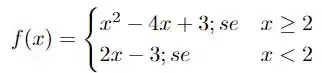
e tal que .
Passo 1
Oiie, tudo certinho?
Precisamos verificar se as funções compostas e existem, assim como, encontrar o domínio e contradomínio das mesmas, por último, devemos também escrever a lei da função, ou seja, seu formato em termos de . Mas como fazemos isso? Vamos definir a composição como
para que exista é necessário que o domínio de seja igual ao contradomínio de ! A análise para é análoga! As nossas funções foram dadas como
tal que
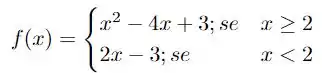
e tal que . Isso é informação suficiente para nossa questão! Vamos lá!
Passo 2
A função tem como domínio todos os reais e também tem como contradomínio todo os reais, é um polinômio de primeira ordem, de domínio real e contradomínio real, sendo assim, ambas as compostas terão domínio e contradomínio real! Só precisamos montar as suas leis! Temos que
Como é definida em dois intervalos, a nossa composta será dividida em duas partes, da seguinte maneira
e
Da mesma forma, temos que a outra composta será dividida em duas partes
e
ou, simplificando, temos que
e
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Temos que e e e . Ambas definidas tal que .