USP – Cálculo 1 – Provas antigas – P1 versão A – 2022.1 – 2
(a)Determinar a função composta se:
(b) Qual é o domínio de ?
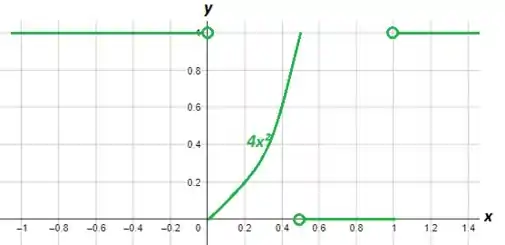
(c) Construir gráfico de .
Passo 1
Eaeeee, belezinha??? Seguinte... a questão nos dá duas funções e e seus respectivos comportamentos e nos pergunta a função composta , o domínio dela e seu gráfico. Lembrando que:
Agora vamos pegar cada intervalo, analisar e aplicar na função composta!!
Passo 2
Dessa forma, como analisamos os valores de para os seguintes intervalos de , representados por 1), 2) e 3):
- Para :
- Para :
- Para :
Dividindo em dois intervalos distintos, temos:
2.1) Para :
2.2) Para :
E, por fim, para o último caso
Dessa forma, temos que:
Passo 3
Na letra (b), como a função apresenta descontinuidade, seu domínio são todos os valores reais de , exceto quando estiver no intervalo , como você verá no gráfico do próximo passo 😉.
Passo 4
Plotando o gráfico e selecionando os intervalos que obtivemos da função composta, temos:
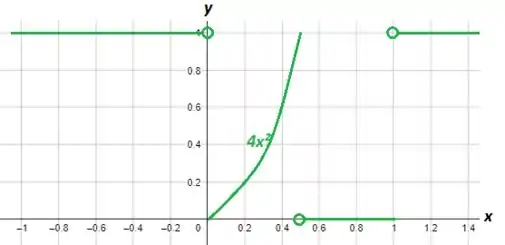
Perceba que:
Entendeu direitinho? Responde aee ;)
Resposta
- como a função não apresenta descontinuidade, seu domínio são todos os valores reais de .
