Questão 3) Desenhe ao menos três curvas de nível e esboce o gráfico da função .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão foi dada uma função e temos que obter algumas curvas de níveis e esboçar o gráfico dessa função.
Vamos por partes! Como podemos esboçar as curvas de níveis da função ?
A ideia desse cálculo é substituir por um número, o qual será o nível que vamos obter sua curva.
A ideia é muito parecida com os mapas topográficos em geografia, lembra deles? Onde representavam os relevos e as montanhas.
Aproveitando a ideia, podemos usar as curvas de níveis pra facilitar a visualização do gráfico da função
Quer ver? Bora lá! 😁
Passo 2
Como dito no passo anterior, temos que esboçar pelo menos três curvas de níveis da nossa função.
Podemos fazer para , e , o que acha?
Para , temos
Ou seja, uma circunferência de raio !
Para , vamos obter a curva
Uma circunferência de raio !
E por último para o nível
Para esse nível, temos uma circunferência de raio !
Esboçando esses níveis no plano , temos
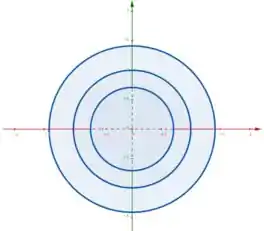
Tranquilo até aqui? 👀
Passo 3
Agora para esboçar o gráfico da função, vamos esboçar essas curvas em seus determinados níveis.
Além disso, vamos obter e esboçar algumas curvas que fazem parte do nosso grafico, como se fossem curvar de níveis verticais.
A ideia da implementação é a mesma, mas dessa vez, vamos determinar valores para e , por exemplo, e .
Substituindo , temos
Encontramos uma parábola voltada para baixo com seu ponto máximo em .
Agora substituindo , temos
Obtemos a mesma curva, mas dessa vez no plano .
Esboçando as curvas de níveis em seus devidos níveis além dessas curvas que acabamos de obter, temos

Dessa forma, podemos imaginar como é o gráfico da função
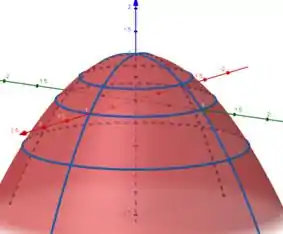
Um paraboloide com a concavidade voltada para baixo!
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
,
,
,