USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.3
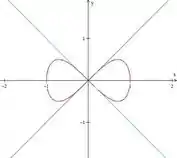
Mostre que a curva tem duas tangentes em (0, 0) e ache suas equações. Faça um esboço da curva.
Passo 1
O vetor tangente a uma curva é dada por
Assim, precisamos encontrar as derivadas de x e y em relação a t e substituir nessa fórmula.
Passo 2
Começando por y:
Agora a derivada de x:
Agora substituindo na formula
Passo 3
Agora a gente precisa descobrir o valor do parâmetro correspondente ao ponto de tangência . Para isso é necessário igualar o ponto à parametrização da curva e resolver o sistema.
Dai temos que
Ou
Ou seja, temos dois valores possíveis para correspondentes ao ponto
Substituindo no vetor tangente, temos
Assim, temos dois vetores tangentes, logo, vamos ter duas retas tangentes no ponto procurado.
Nossa equação da reta tangente fica então igual a:
E
Resposta
Exercícios de Livros Relacionados
D e t e r m i n e o p o l i n ô m i o d e T a y l o r , d e o r d e m 2 , d e f e m v o l t a d e x_0 d a d o . ô sen x e x_0 = 0
D e t e r m i n e o p o l i n ô m i o d e T a y l o r , d e o r d e m 2 , d e f e m v o l t a d e x_0 d a d o . ô f (x) = cos x e x_0 = 0
Utilizando a relação s e nx = x + o x 2 ,c a l c u l elim x → 0 s e nx - x 2 x 2 Sugestão. o x 2 é um infinitésimo de ordem superior a x 2 , para x → 0 , isto é, lim x → 0 o x 2 x 2 = 0
38. Sejam P x e Q x polinômios tais que P ( x 0 ) =P ' x o = 0 ,Q ( x 0 ) = Q ' ( x 0 ) = 0 e Q " ( x 0 ) ≠ 0 . Mostre que lim x → xo P x Q x = P " x o Q " x o . Generalize.
Utilizando a relação s e nx = x + o x 2 ,c a l c u l e lim x → 0 sen x - x x 2 Sugestão. o x 2 é um infinitésimo de ordem superior a x 2 , para x → 0 , isto é, lim x → 0 o x 2 x 2 = 0