USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 1
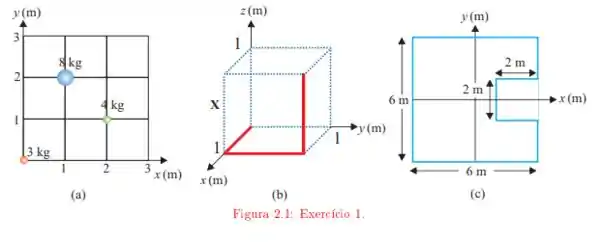
Ache as coordenadas do centro de massa das figuras seguintes. Em considere que os fios tem a mesma densidade linear de massa uniforme. Em considere que a densidade superficial de massa é uniforme.
Passo 1
Oii, tudo bem com você?
Temos o esquema de três distribuições de massa
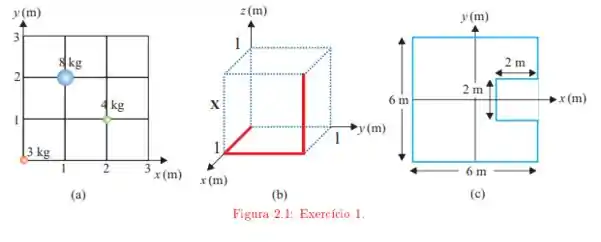
precisamos obter as coordenadas do centro de massa de cada uma delas. Na distribuição os fios tem distribuição linear de massa e na distribuição a figura é uma distribuição homogênea de massa. A primeira situação é um caso direto em que podemos calcular discretamente a coordenada através da relação
Para a segunda situação precisamos utilizar a seguinte relação para as coordenadas
, e
que nos dá as coordenadas para cada fio! Mas será que isso nos dá diretamente as coordenadas do sistema como um todo? Pense um pouco sobre isso! Para o última sistema precisamos considerar um sistema em que retiramos parte da massa! Em um quadrado homogêneo, onde normalmente estaria o centro de massa? Consegue adivinhar? Vem comigo!
Passo 2
Começando pela primeira figura, temos que
, e
portanto, temos que
temos que está na origem, portanto , também temos observando a figura que e . Portanto, temos que
Finalmente, podemos escrever que
Vamos para a próxima agora!
Passo 3
Para todos os três fios podemos escrever que
em que pode ser tanto ou . Vamos fazer para o fio que está sobre o eixo , temos que o seu centro de massa é dado por
ou simplesmente
Como temos que a distribuição linear é uniforme, podemos dizer que
e, portanto, o centro de massa desse fio está em
os outros dois fios são equivalentes, mas trocando por e por , de forma que temos que
e, sendo assim, como os três têm a mesma massa, a coordenada do centro de massa é dada por
Vamos para a última distribuição agora!
Passo 4
Note que a distribuição é um quadrado do qual foi retirado um quadradinho menor. Se o quadrado é homogêneo, o seu centro de massa é no centro! Portanto, originalmente o quadrado completo teria centro de massa em
exatamente na origem! No entanto, o quadradinho menor tinha um centro de massa próprio em seu centro dado por
quando retiramos um pedaço da massa, o deslocamento do centro de massa pode ser calculado normalmente, mas com um massa “negativa”, ou seja, o novo centro de massa será dado por
Vamos achar essas massas agora!
Passo 5
A distribuição de massa superficial é constante, portanto, temos que
Através do gráfico, temos que
e
Portanto, obtemos que
Substituindo esse resultado na expressão para a coordenada do centro de massa, temos que
ou simplesmente
Uff… A questão foi isso! Te vejo na próxima! Tchau Tchau!