UFABC – Fenômenos Mecânicos – Lista 5 – Questão 09
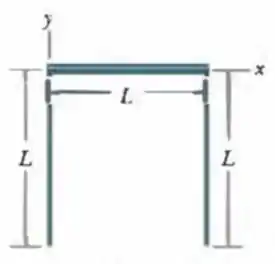
Na figura mostrada a seguir, três barras finas e uniformes, de comprimento , formam um invertido. Cada barra vertical tem uma massa de ; a barra horizontal tem massa de . Quais são
(a) a coordenada e
(b) a coordenada do centro de massa do sistema?
Passo 1
Oi, galerinha! Tudo bom? O problema nos deu um sistema composto por 3 barras homogêneas e nos pediu para calcular o centro de massa. Bom, como as barras são homogêneas, o centro de massa de cada uma delas vai ser bem na metade.
aí para calcular o centro de massa do sistema, a gente pode usar as fórmulas do centro de massa, com os dados de cada uma das barras. Mas relaxa, vou fazer passo a passo com você!
Vamos lá?
Passo 2
Para calcular a coordenada de cada eixo do centro de massa podemos usar as seguintes relações:
Onde, é a massa de cada partícula, é a posição do centro de massa no eixo e é a posição do centro de massa no eixo .
Commentei ali antes, mas é bom reforçar, para barras homogêneas o centro de massa se encontra bem no centro dela!
Agora vamos calcular! Primeiro a massa total:
Passo 3
Letra (a): Agora a coordenada :
Vamos olhar novamente o desenho e verificar onde estão as coordenadas dos centros das três barras:
As barras verticais tem massa e a barra deitada tem massa , então agora é só substituie:
Beleza? Agora precisamos repetir esse raciocínio para a coordenada !
Passo 4
Letra (b): voltando na figura, as coordenadas verticais dos centros das barras são:
Assim:
E essa é a coordenada y do centro de massa do conjunto!
Beleza? Espero ter ajudado!
Resposta
- ;
- .