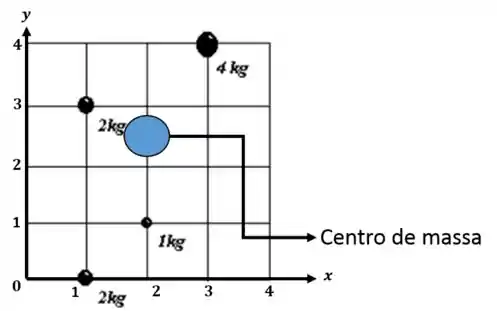
Calcule o centro de massa do objeto esquematizado na figura abaixo (despreze a massa da grade):
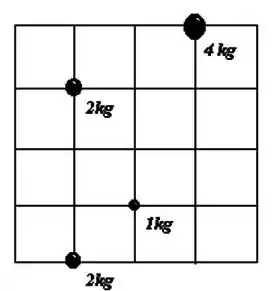
Passo 1
O primeiro passo é escolher um referencial e um sistema de medida. Vamos adotar aqui que os lados de cada quadrado da grade valem 1u.
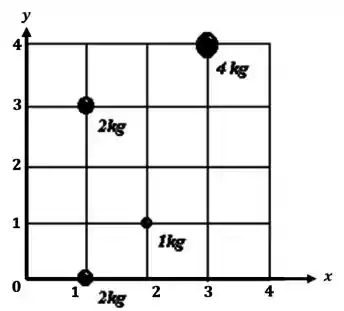
Passo 2
Agora precisamos da posição de cada um dos objetos.
Temos a posição para o objeto de massa .
Temos as posições e para os objetos de massa de .
Temos a posição para o objeto de massa .
Passo 3
Agora é só aplicar a fórmula para achar a posição do centro de massa.
Agora podemos ilustrar onde está o centro de massa.
Resposta
Exercícios de Livros Relacionados
A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
Um pedaço uniforme de folha de metal é moldado conforme mostrado na Figura P8.34. Calcule as coordenadas x e y do centro de massa da folha.
Uma haste de 30,0c m de comprimento tem densidade linear (massa por comprimento) definida por λ=50,0+20,0x em que x é a distância a partir de uma extremidade, medida em metros, e λ expressa g r a m a
Duas partículas de 3,0k g têm velocidades v → 1 = 2,0 m s i ^ + 3,0 m s j ^ e v → 2 = 4,0 m s i ^ - 6,0 m s j ^ . Encontre a velocidade do centro de massa do sistema.
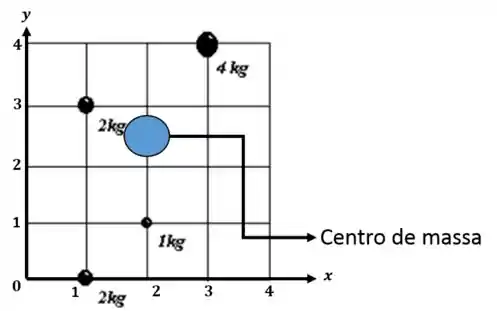
Quatro corpos estão situados ao longo do eixo y da seguinte forma: um de 2,00k g está a + 3,00m , um de 3,00k g está a + 2,50m , o terceiro, de 2,50k g , está na origem, e o quarto, de 4,00k g , está