Uma corrente é mantida sobre uma mesa sem atrito, com de seu comprimento pendurado fora da mesa, conforme a figura abaixo. Se a corrente tem comprimento e massa , qual o trabalho necessário para puxá-la totalmente para cima da mesa?
a)
b)
c)
d)
e)
Passo 1
Pra trazer esse pedacinho de corda pra cima o trabalho de uma força externa será a variação de energia potencial desse pedacinho
Passo 2
Agora temos que calcular a variação de energia potencial desse pedacinho. O centro de massa desse pedacinho será bem no seu meio, em conforme a figura
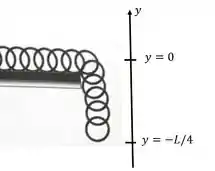
A massa desse pedaço é da massa total da corda, ou seja, .
Assim a variação de energia potencial pra trazer o pedaço de corda para mesa será
Resposta
D
Exercícios de Livros Relacionados
A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
Um pedaço uniforme de folha de metal é moldado conforme mostrado na Figura P8.34. Calcule as coordenadas x e y do centro de massa da folha.
Uma haste de 30,0c m de comprimento tem densidade linear (massa por comprimento) definida por λ=50,0+20,0x em que x é a distância a partir de uma extremidade, medida em metros, e λ expressa g r a m a
Duas partículas de 3,0k g têm velocidades v → 1 = 2,0 m s i ^ + 3,0 m s j ^ e v → 2 = 4,0 m s i ^ - 6,0 m s j ^ . Encontre a velocidade do centro de massa do sistema.
Quatro corpos estão situados ao longo do eixo y da seguinte forma: um de 2,00k g está a + 3,00m , um de 3,00k g está a + 2,50m , o terceiro, de 2,50k g , está na origem, e o quarto, de 4,00k g , está