UFABC – Fenômenos Mecânicos – Lista 5 – Questão 10
Na molécula de amônia () da fogira mostrada a seguir, três átomos de hidrogênio (H) formam um triângulo equilátero, com o centro do triângulo a uma distância de cada átomo de hidrogênio. O átomo de nitrogênio (N) está no vértice superior de uma pirâmide, com os três átomos de hidrogênio formando a base. A razão entre as massas de nitrogênio e do hidrogênio é e a distância nitrogênio-hidrogênio é . Quais são as coordenadas
(a) e
(b) do centro de massa da molécula?
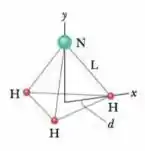
Passo 1
Oi, galerinha! Tudo bom? O problema nos deu um sistema composto por 3 barras homogêneas e nos pediu para calcular o centro de massa. O centro de massa é como se fosse a média entre as coordenadas e as massas das partes do sistema. No nosso caso temos três átomos de hidrogênio e um de amônia.
O interessante aqui é a gente perceber que temos simetria! A base forma um triângulo equilátero e com os dados, podemos achar a altura da molécula de .
A fórmula do centro de massa é:
Porém, devemos prestar atenção para o caso de haver simetria na peça (e aqui tem!). Neste caso, percebemos que o eixo corta exatamente nossa peça ao meio (!!).
Mas relaxa, vou ajudar você aqui!
Vamos lá?
Passo 2
Letra (a): vamos começar calculando a coordenada x do centro de massa.
Pela questão de simetria que falei ali no passo anterior, para calculcar a coordenada do centro de massa não precisamos aplicar a expressão da da no passo anterior. Devemos perceber que o centro de massa da peça está localizado no eixo de simetria que é o eixo . Já que a base forma um triângulo equilátero e o átomo de N está bem no centro ao longo do eixo .
Assim:
Beleza? Agora vamos para o cálculo da coordenada y!
Passo 3
Letra (b): Para determinar a coordenada do centro de massa, usaremos a expressão dada no passo inicial:
As coordenadas dos hidrogênios são todas nulas, já que esses átomos estão no chão.
Assim temos:
Podemos isolar , que é a componente do Nitrogênio. Aí temos o seguinte:
Tranquilo? Agora vamos voltar para o desenho!
Passo 4
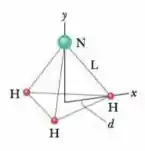Vamos rever o desenho:
Como o desenho é formado por triângulos retângulo, podemos aplicar o teorema de pitágoras para determinar o . A hipotenusa do triângulo é o , um dos catetos é a distância e é o outro. Dai temos
E substituindo os valores dados:
E foi dado que a relação entre a massa de nitrogênio e de hidrogênio é . Aí podemos resgatar a equação para do passo anterior
E substituir e :
E isolando :
Por fim temos :
E essa é a coordenada do centro de massa dessa molécula!
Ufa! Terminamos! Espero ter ajudado!
Resposta
- ;
- .