Uma bolinha de raio desprezível e massa , é colocada na borda de um disco de raio e massa . A que distância do centro do disco encontra-se o Centro de Massa desta configuração?
Passo 1
Bem... Primeiro, acho interessante a gente desenhar, neh? Assim a gente tem uma visão geométrica do que está acontecendo.
Inicialmente temos apenas um disco de raio ...
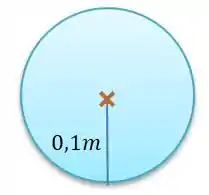
Como o disco tem uma distribuição de massa uniforme, o centro de massa dele está na origem ().
Mas em certo momento a gente coloca uma bolinha de raio desprezível na borda de massa ...
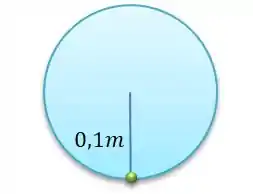
Certamente a presença dessa bolha de massa desloca o centro de massa um pouquinho para baixo:
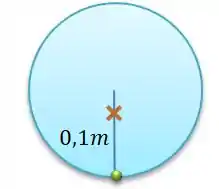
A gente quer saber agora de quanto foi esse deslocamento.
Passo 2
POW! De acordo com a teoria, podemos descobrir o novo centro de massa () se a gente conhecer o cento de massa de cada um dos envolvidos e as suas massas também pela formulinha...
Se tivéssemos mais bolinhas, era só ir acrescentando em cima e em baixo, ta ligado?
Bem, é o centro de massa do disco e é a sua massa. Para a bolinha, que é o seu centro de massa e . Então, o novo centro de massa do conjunto, será...
Então o centro de massa deslocará para baixo!
Resposta
Letra B.