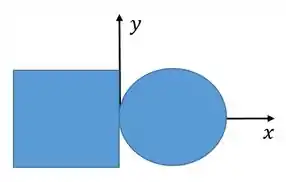
Considere o sistema formado por duas placas, uma circular de diâmetro , e outra quadrada de lado . O ponto de contato entre as placas é meio da aresta como indicado na figura, e a origem do sistema é definido nesse ponto. Se ambas as placas têm a densidade superficial igual e uniforme, as coordenadas do ponto de centro de massa (CM) do sistema é dado por:
a) e
b) e
c) e
d) e
e) e
Passo 1
Meio que de cara já sabemos que a posição do centro de massa de cada um desses objetos é no seu centro geométrico, assim
E pro quadrado
Como pros dois a posição no eixo é nula então a posição do centro de massa do sistema é
Já temos 1! Só falta a !
Passo 2
A posição do centro de massa é dada por
Então precisamos da massa de cada um deles! Só que não temos no enunciado...... Só sabemos que as densidades superficial de massa dos dois são iguais, assim, chamando a densidade superficial de massa de
E então
E as áreas sabemos calcular! \o/
Finalmente
Resposta
D