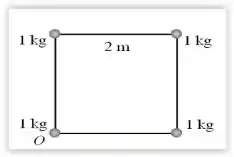
Calcule as coordenadas (xcm, ycm) do centro de massa do sistema de partículas da questão 17. Considere o ponto O como sendo a origem do sistema de coordenadas (x,y).
(A) (1,0m, 1,0m)
(B) (1,0m, 1,5m)
(C) (1,5m, 1,5m)
(D) (1,5m, 0)
(E) (1,5m, 1,0m)
Passo 1
Você lembra da fórmula de centro de massa?
Ela também pode ser destrinchada para cada eixo:
Começando por , vamos aplicar:
Repare que as partículas do lado esquerdo têm uma distância em x nula até O, enquanto as partículas de baixo têm uma distância em y nula até O.
Aplicando para :
- ''Resposta
(A) (1,0m, 1,0m)