Considere a molécula d’água com seus três átomos distribuídos com localizações fixas de acordo com a figura abaixo, sendo a distância entre o átomo de Oxigênio (O) e um átomo de Hidrogênio (H). Encontre o vetor posição do centro de massa da molécula, em relação à posição do átomo de Oxigênio, em função da distância .
Sabe-se que , , , e (unidades de massa atômica).
Passo 1
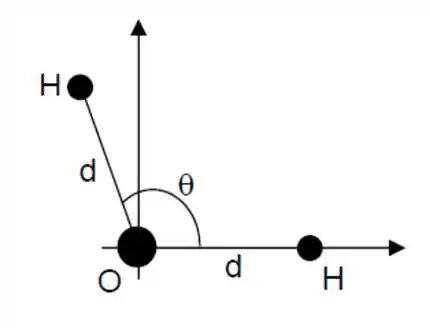
A primeira coisa que temos que fazer é deixar claro quais são nossos eixos!
Temos que calcular a posição do centro de massa do sistema em relação ao átomo de oxigênio O então O é a nossa origem. O eixo aponta pra direita e o eixo aponta pra cima.
Repare que as coordenadas do hidrogênio da direita são . Vou chamá-lo de , ok?
Mas ainda precisamos achar as coordenadas do outro hidrogênio, o !
Passo 2
Sabemos que então o ângulo entre o eixo e o é . Não é à toa que deram pra gente e no enunciado! Então queremos as coordenadas e do átomo de hidrogênio:
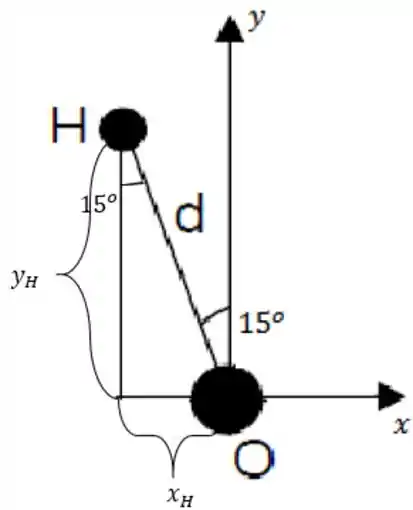
Olhando o triângulo formado na esquerda e aplicando trigonometria básica, temos:
Mas como o eixo aponta pra direita, a coordenada do átomo é .
Passo 3
Vamos calcular a posição do centro de massa! :D
Recapitulando, as coordenadas dos 3 átomos são pro oxigênio, pro e pro .
Vamos começar pela coordenada do centro de massa:
e , então isso dá
Substituindo isso dá:
Passo 4
Show, agora vamos achar a coordenada do !
Usando temos
Então é isso! Sendo o vetor unitário do eixo e o vetor unitário do eixo , o vetor posição do centro de massa da molécula, em relação à posição do átomo de oxigênio é:
.