Uma haste homogênea muito fina de massa e de comprimento pode girar livremente num plano vertical, em torno de um pino que atravessa a haste a uma distância de uma de suas extremidades. A haste, que se encontrava inicialmente na posição vertical, com seu centro de massa acima do pino, é posta a girar no sentido horário, a partir do repouso. O trabalho do peso sobre a haste entre o instante inicial e o instante em que a haste passa pela posição horizontal é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Passo 1
Vamos entender melhor o que está acontecendo.
Temos uma haste presa por um pino a uma distância de do canto dela. Além disso, a haste está na vertical para cima:
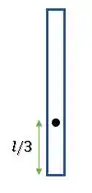
Queremos saber o trabalho da força peso se a haste girar no sentido horário até a horizontal:
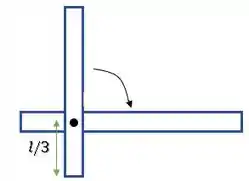
Okay, mas aonde está a força peso nesse cara?
Podemos concentrar a força peso em seu centro de gravidade.
Como a haste é homogênea, sua massa está uniformemente distribuída e com isso podemos dizer que seu CG está no centro da haste.
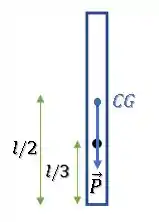
Então, basta calcular o trabalho da força peso nesse movimento.
Passo 2
Bom, o trabalho da força peso é dado por:
Sabemos que ele só depende da variação de altura do corpo, nesse caso do centro de gravidade do corpo.
Qual foi a variação de altura do centro de gravidade?
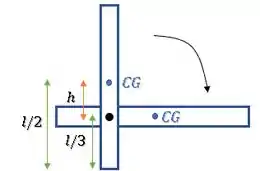
Considerando o referencial no ponto mais baixo da barra quando ela está na vertical, o CG se encontra a uma altura igual à metade do comprimento da barra , e depois da rotação, ele se encontra na mesma altura do pino , então:
Agora que achamos a variação de altura do centro de gravidade, vamos calcular o trabalho da força peso.
Como o o centro de gravidade está “descendo”, a força peso está a favor do movimento e por isso seu trabalho será positivo:
Ficamos, então, com a letra (e).
Resposta
Letra (e)