Encontre a posição do centro de massa da chapa abaixo de raio , sabendo que foi feito um furo dela de raio posicionado como indicado na figura. Considere também que a chapa é homogênea.
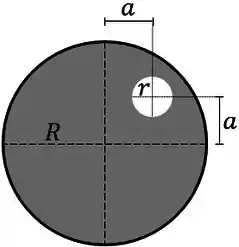
Passo 1
Nesse exercício temos um problema. Normalmente quando vamos achar o centro de massa separamos em retângulos certo? Tendo círculos ali não tem problema, o centro de massa de um círculo é no seu centro. O grande problema é aquele buraco.
Quando estivermos lidando com objetos que perdem um pedaço, podemos considerar o sistema como sendo o objeto original+furo, onde o furo tem massa negativa, como vimos na teoria.
Passo 2
Como resolvemos isso então?
Repara que temos dois círculos, então colocando o eixo cartesiano como mostrado abaixo
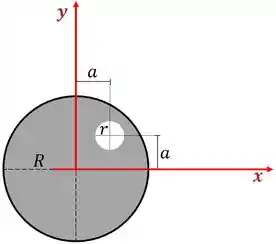
Vamos ter
e
e
Como ele não determinou os eixos, não importa qual eixo vou escolher. Eu decidi pelo eixo que passa pelo centro do disco maior para termos contas mais fáceis, mas não faz diferença.
Passo 3
Pela fórmula do centro de massa, a posição do centro de massa no eixo é
Repara o sinal negativo para o disco de raio !!
Passo 4
A posição do centro de massa no eixo é
Passo 5
Então o vetor do centro de massa fica
No sistema de eixos que escolhemos.
Uma forma de escrever isso onde o eixo não importe é deixar indicado que
“O centro de massa encontra-se a abaixo e a para esquerda do centro do disco maior”
Resposta
“O centro de massa encontra-se a abaixo e a para esquerda do centro do disco maior”