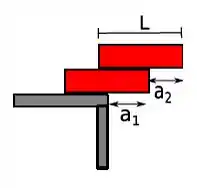
Dois tijolos homogêneos, de massas M e de comprimentos L, estão empilhados sobre o canto de uma mesa, um sobre o outro, como na figura ilustrativa abaixo. Quais são os maiores comprimentos possíveis a1 e a2 para que a pilha permaneça em equilíbrio?
a) a1 = L/4; a2 = 2L/3
b) a1 = L/4; a2 = L/2
c) a1 = L/2; a2 = 3L/4
d) a1 = 4L/3; a2 = L/2
e) a1 = L/3; a2 = 4L/5
f) a1 = 5L/2; a2 = L/2
g) a1 = L/2; a2 = 2L/3
h) a1 = L/2; a2 = L/3
Passo 1
O centro de massa do tijolo de cima não pode passar da beirada do tijolo de baixo. Porque se não o momento resultante devido à força peso ia ser diferente de zero, e iria tudo desmoronar! Então:
Lembrando que a posição do centro de massa é em L/2.
Passo 2
Com o mesmo pensamento, o centro de massa dos dois tijolos juntos não pode passar da beirada da mesa. O centro de massa dos dois juntos é, se a gente colocar um sistema de coordenadas com origem no ponto inferior esquerdo do tijolo de baixo:
Repare que aqui eu já usei o valor de .
O valor de vai ser então:
Resposta
Letra B.