Encontre a posição do centro de massa da chapa abaixo, considere a chapa homogênea.
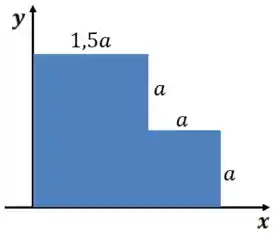
Passo 1
Essa chapa é o nosso sistema, podemos então “quebrá-la” em vários objetos que sabemos o centro de massa, mas quais são esses objetos? Retângulos, o centro de massa de retângulos é exatamente no seu meio. Separando essa figura temos
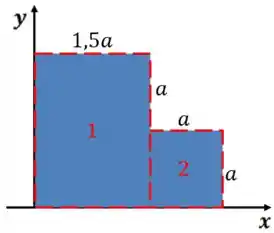
Vamos ter as seguintes componentes para o centro de massa dos retângulos (coordenadas do centro do retângulo):
Passo 2
Quando cada objeto na verdade são chapas, podemos usar a área de cada uma delas em vez da massa, isso porque elas são proporcionais
Assim, vamos calculas a posição do centro de massa
Passo 3
Agora, vamos calcular a posição do centro de massa
Passo 4
O vetor centro de massa fica
Resposta
Exercícios de Livros Relacionados
A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
Um pedaço uniforme de folha de metal é moldado conforme mostrado na Figura P8.34. Calcule as coordenadas x e y do centro de massa da folha.
Uma haste de 30,0c m de comprimento tem densidade linear (massa por comprimento) definida por λ=50,0+20,0x em que x é a distância a partir de uma extremidade, medida em metros, e λ expressa g r a m a
Duas partículas de 3,0k g têm velocidades v → 1 = 2,0 m s i ^ + 3,0 m s j ^ e v → 2 = 4,0 m s i ^ - 6,0 m s j ^ . Encontre a velocidade do centro de massa do sistema.
Quatro corpos estão situados ao longo do eixo y da seguinte forma: um de 2,00k g está a + 3,00m , um de 3,00k g está a + 2,50m , o terceiro, de 2,50k g , está na origem, e o quarto, de 4,00k g , está