Considere a placa circular de densidade uniforme, de raio , com um buraco quadrado de lado , conforme mostrado na figura 4. Em coordenadas de acordo com os eixos e da figura, onde está localizado o centro de massa da placa?
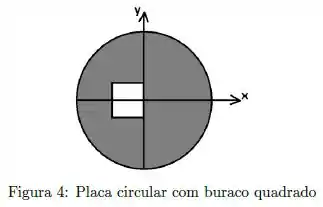
(A) ; e
(B) ; e
(C) ; e
(D) ; e
(E) ; e
Passo 1
O enunciado diz que o disco tem densidade uniforme, ou seja, homogênio. Isso é o mesmo que dizer que a massa do disco é uniformemente distribuida.
Então, se o disco não tivesse furo algum, seu centro de massa seria no centro do disco, devido à sua simetria.
Porém, temos um furo quadrado. Então, a massa está mais concentrada do lado direito e seu centro de massa está deslocado também para a direita :
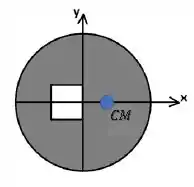
OBS: O disco ainda é simétrico com relação ao eixo , então seu centro de massa terá coordenada .
Mas como calculamos a coordenada ?
Podemos usar um truque que simplifica nossas contas...
Quando temos uma placa furada, podemos considerar dois objetos que conhecemos a posição do centro de massa e fazer a posição do CM entre eles.
E quem seriam esses dois objetos?
O primeiro seria o disco sem o furo, onde o CM está no centro do disco.
E o segundo seria o furo quaadrado, onde seu CM está no centro do quadrado... porém, sua massa entra na conta como negativa.
Aí a conta seria a seguinte:
Passo 2
Vamos começar com as posições do CM do disco e do quadrado.
Como o centro do disco está na origem, sua coordenada é:
Já o quadrado tem lado , então seu centro está a uma distância de meio lado para a esquerda:
Passo 3
Agora, vamos às massas.
A massa do disco sem furo nós chamamos de .
Vamos calcular a massa do quadrado com relação a esse valor, lembrando que ela será negativa, pois na verdade é uma massa ausente.
Vamos usar uma simples regra de 3 com proporção entre a área do disco e a área do quadrado.
A área do disco é:
Já a área do quadrado é:
Então, a regra de 3 fica assim:
Então, a massa do quadrado será:
Passo 4
Agora podemoas aplicar aquela fórmula para calcular o centro de massa do disco mais o furo:
Calma, essa expressão monstruosa melhora bastante.
Multiplicando as frações de cima e colocando o em evidência em baixo, temos:
O numerado vezes o inverso do denominador:
Cortando com , com , e com , temos:
Ah, último detalhe... aquele dividindo vira multiplicando para a resposta ficar igualzinha hahah:
Prontinho, achamos as coordenadas e do centro de massa da placa furada:
Resposta
Letra (C)