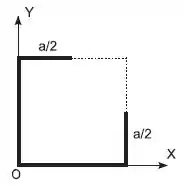
Um arame homogêneo e uniforme, de espessura desprezível, é moldado na forma de um quadrado de aresta Retira-se então um segmento de comprimento de duas arestas , reduzindo-as à metade, como mostra a figura. No novo sistema a distância do centro de massa à origem é igual a,
Passo 1
Para achar a distância do centro de massa até a origem devemos achar a posição do centro de massa e fazer o módulo desse vetor.
Ao usar arames, vamos considerar em vez da massa, o seu comprimento. Isso porque a massa e o comprimento são proporcionais, então no cálculo do centro de massa não altera o resultado.
O eixo cartesiano já foi dado pelo enunciado, então vamos nos basear nele.
Repara que o novo sistema é composto por 4 arames, vamos numera-los para nos organizar.
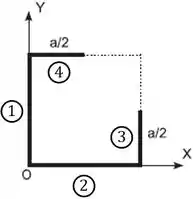
Passo 2
Lembra que o centro de massa de um arame é no seu “meio”? Então:
Passo 3
Usando a fórmula para as coordenadas do centro de massa vamos ter
Lembrando que
Assim
Passo 4
Agora fazendo no eixo
Então teremos
Passo 5
O vetor posição do centro de massa vai ser
A distância do centro de massa até a origem é o módulo do vetor posição, já que o vetor posição parte da origem.
Resposta
Letra