UFSC, Araranguá, Física 1, P3 - 2021.2, Questão 3
Calcule a partir da origem do sistema de coordenadas, as coordenadas do centro de massa da placa homogênea abaixo:
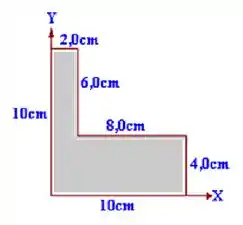
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma placa homogênea posicionada em um sistema de coordenadas , com suas dimensões, e pediu pra gente calcular as coordenadas do centro de massa dessa placa. Pra isso, nós vamos começar dividindo a placa em três partes uniformes, assim:
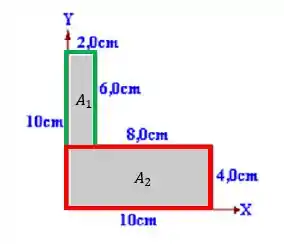
Como a placa é toda homogênea, a massa de cada uma de suas partes é proporcional a sua área, e o centro de massa da placa inteira é dado por:
Show! Então, o que nós precisamos é encontrar as áreas e os centros de massas para cada peça.
Vamos lá!
Passo 2
Vamos começar calculando as áreas de cada uma das partes:
Já podemos achar a área total, que entrará no denominador no cálculo das coordenadas:
Agora só precisamos achar os centros de massa.
Passo 3
Nas figuras retangulares, os centros de massa são bem no centro dos retângulos, certo?
Vamos calcular cada coordenada do centro de cada retângulo dividindo cada lado por . No retângulo :
No retângulo :
Passo 4
Agora só nos resta aplicar todos os valores que encontramos nas fórmulas do passo para cada coordenada:
Prontinho, galera! Até a próxima! 😉