Um sistema é formado por 4 partículas que se encontram nos vértices de um quadrado de lado , conforme mostra a figura.

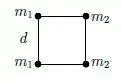
Sabendo que , qual a situação que representa a posição do centro de massa do sistema?

A posição do centro do centro de massa desse sistema de partículas vai ser nada mais do que uma média ponderada da posição de cada partícula do sistema, onde as massas de cada uma dessas partículas serão os pesos dessa média ponderada.

Tá bom, muita fala para um negócio bem simples...

Basicamente, o centro de massa estará mais próximo de onde estiver mais massa no sistema.

Vamos considerar um sistemas de eixos com a origem ali na partícula inferior esquerda:

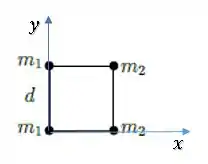
Podemos calcular as coordenadas e desse centro de massa separadamente, usando:

Vamos começar com a coordenada do eixo :

Como :

Agora, vamos calcular a coordenada em :

Novamente, utilizando a relação :

A partir da coordenada , vemos que o centro de massa se encontra na metade da altura do quadrado , enquanto sua distância horizontal da origem deve ser um quarto do lado do quadrado e por isso dista três quartos do lado direito.

Essas coordenadas representam a posição da letra (a).