UNICAMP – Física 1 2019.2 – Exame – Questão 1
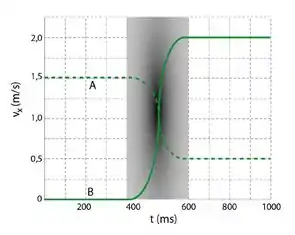
A figura ao lado representa o gráfico da velocidade por tempo para dois objetos, e , de massas e , respectivamente, que se movem em linha reta num trilho de atrito desprezível, antes e após eles colidirem entre si. O objeto B está inicialmente em repouso.
- Determine a velocidade do centro de massa do sistema antes e após a colisão.
-
A sobre o objeto durante a colisão.
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Essa primeira questão fala sobre colisões, certo? E ela nos pede a velocidade do centro de massa antes e depois da colisão. Bom, como o momento linear é sempre conservado, então a velocidade do centro de massa também é!
Mas como a gente calcula essa velocidade? É só lembrar dessa fórmula aqui ó, levando em conta dois objetos e :
Os dados que o problema nos trás são os seguintes para o momento antes da colisão:
Pronto! Agora é só substituir:
Tranquilo até aqui? Vamos para o item (b)?
Passo 2
Agora o exercício nos pede para calcular a força média exercida pelo objeto sobre o objeto , e aqui preciso fazer uma observação: a força que queremos é NO objeto , então vamos usar a massa do objeto .
E como a gente calcula a força mesmo? AH! Lembrando lá de leis de Newton, sabemos que a força é proporcional à aceleração que o corpo sobre, certo? Então precisamos calcular aceleração que esse corpo sofreu!
Passo 3
A partir do gráfico, podemos ver que o objeto partiu do repouso e adquiriu uma velocidade de após a colisão. E tudo isso em um intervalo de tempo de... de quanto tempo? Tudo que vemos no gráfico? Todo intervalo? Nãããão! Apenas o tempo decorrente da colisão! A colisão levou do instante até o , não é? Então o intervalo de tempo eu queremos é de:
Agora sim podemos calcular a força, já que temos a variação da velocidade, o intervalo de tempo e a massa do objeto :
Beleza?
Pronto pra próxima questão? =)