Dois blocos, de massas e , movem-se sobre um plano horizontal sem atrito com vetores posição dados como função do tempo respectivamente por e, com todas as unidades no SI. (Se julgar necessário, utilize o par de eixos ao lado como auxílio.)

(a) Para o instante , encontre, em termos dos vetores unitários, o vetor posição do centro de massa.

Considerando que os blocos colidem de modo totalmente inelástico, calcule:

(b) o ângulo entre o vetor velocidade do conjunto e o semieixo positivo .

Considerando uma outra colisão em que o segundo bloco adquire velocidade final, calcule:

(c) o vetor velocidade final do primeiro bloco, em termos dos vetores unitários.

b)

Agora, os blocos colidiram de maneira totalmente inelástica, isso quer dizer que no final da colisão eles saem colados!

O momento linear se conserva, afinal não temos forças externas atuando no sistema. Então

Eita... não sabemos as velocidades nos corpos 1 e 2... E agora? Ah, tudo tranquilo! Podemos descobrir, pois a velocidade é a derivada, em relação ao tempo, da posição.

Mesma coisa para o corpo 2:

Voltando lá na equação de conservação do momento:

Beleza. Já sabemos o vetor velocidade final. Mas queremos o ângulo que esse vetor faz co o eixo x. Podemos encontra isso através do produto escalar de com .

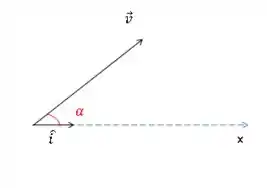
Mas o produto escalar também é igual ao produto de componente a componente dos vetores:

Então no nosso caso:

Beleza, voltando para a outra equação:

O é 1, pois ele é um vetor unitário. E

Então

Dessa forma

Então

c)

Agora, ao invés deles terem colidido de forma totalmente inelástica, vamos considerar um colisão na qual a velocidade final dos blocos não são iguais. Beleza?

O momento linear se conserva, pois não há força externa.

Então

Maravilha!