UTFPR, Sem Campus, Física 1, Listas de Física 1 - UTFPR - Lista 3 - Sistemas de partículas, Questão 3
Três pequenas esferas, , e , com as massas de , e , respectivamente, estão montadas nos vértices de um triângulo de hastes rígidas, muito leves. As coordenadas das esferas no plano são: , e .
a) Desenhe o sistema no plano ;
b) Que coordenada tem o centro de massa? Indique a posição do centro de massa no desenho da letra a).
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos pediu pra gente desenhar o sistema de três esferas com as coordenadas que ele nos deu e encontrar o centro de massa desse sistema.
Para encontrar as coordenadas do centro de massa do sistema, temos que lembrar que, em geral, a posição do centro de massa de um sistema é dado pela média ponderada da posição dos objetos no sistema, considerando sua massa. Seria o seguinte:
Onde representam a posição do centro de massa do objeto respectivamente. Além disso, , então também podemos separar os eixos para calcular.
Vamos lá!
Passo 2
Vamos começar usando as coordenadas , e , para plotar o sistema no plano cartesiano , em metros:
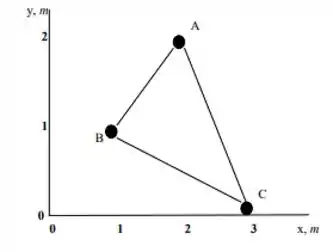
Passo 3
Agora vamos calcular as coordenadas do centro de massa do sistema, começando com o eixo . Vamos considerar as coordenas , e e as massas , e . Fica assim:
Substituindo as coordenas e as massas:
Agora calculando a coordenada , vamos ter:
Substituindo os valores dados:
Portanto, nosso centro de massa se encontra no ponto , como mostra a bolinha azul na figura:
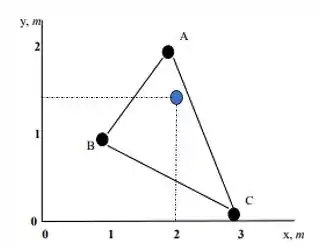
Valeu, galera! Até a próxima! 😉