UTFPR, Sem Campus, Física 1, Listas de Física 1 - UTFPR - Lista 3 - Sistemas de partículas, Questão 4
A massa da folha de compensado é de . Qual a localização do centro de massa? Faça um desenho indicando a posição calculada.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a localização do centro de massa do sistema e pra isso nós precisamos determinar suas coordenadas .
Para encontrar as coordenadas do centro de massa do sistema, temos que lembrar que, em geral, ele é dado pela média ponderada da posição dos objetos no sistema, considerando sua massa. Seria o seguinte:
Mas a gente também pode considerar a média em função das áreas dos objetos, nos casos em que tenhamos a mesma densidade superficial. Isso vai ser útil pra gente porque vamos dividir nossa folha de compensado em três retângulos e, como sabemos apenas a massa total da folha, vamos considerar a área de cada um desses retângulos no cálculo das coordenadas do centro de massa.
Vamos lá!
Passo 2
Vamos começar dividindo nossa figura em três retângulos, que chamaremos de , e e colocando ela no plano cartesiano :
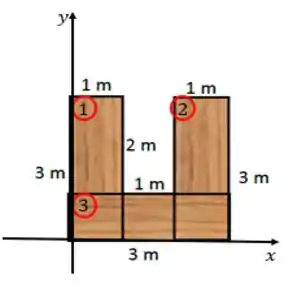
Em figuras simétricas, como o retângulo, o centro de massa do sistema se localiza em seus eixos de simetria. Então, no caso do retângulo vamos ter o centro de massa no meio de sua base e altura.
Sendo assim, para o retângulo , de acordo com as coordenadas do plano e os comprimentos mostrados na figura, temos o centro de massa em:
Além disso, como sua altura é igual a e base igual a , temos a área . De modo semelhantes, vamos ter no retângulo :
E área . E por fim, para o retângulo , ali deitadinho no plano, temos a área e as coordenadas do centro de massa em:
Passo 3
Agora vamos calcular as coordenadas do centro de massa do sistema, levando em consideração o centro de massa de cada retângulo e suas respectivas áreas. Fica assim:
Substituindo as coordenas e as áreas:
Agora calculando a coordenada , vamos ter:
Substituindo os valores de as áreas calculadas:
Portanto, o centro de massa da folha de compensado se encontra no ponto , como mostra a figura:
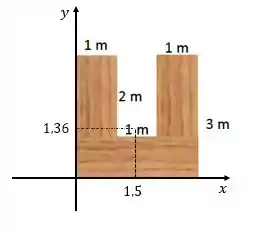
Valeu, galera! Até a próxima! 😉