Exercícios Resolvidos de Reta Tangente e Normal a Curva

Ver Teoria

Exercício 39 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

Enunciado

UFF, Sem Campus, Cálculo IIB, P1 - Prof. Jorge Delgado - 2023 - Verão, Questão 2c

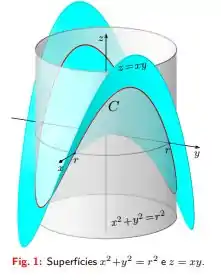
Seja a curva fechada dada pela interseção das superfícies de equações cartesianas e (Fig. 1).

Determine os pontos da curva onde a reta tangente é horizontal (paralela ao plano ).

Passo 1

Eaew, tudo certinho contigo?

Temos uma curva obtida pela interseção entre as superfícies e , a interseção ocorre como na figura

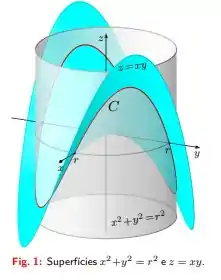
precisamos encontrar os pontos no qual a reta tangente a curva é horizontal (paralela ao plano ) isso ocorre quando o vetor inclinação da reta é perpendicular ao versor que indica a direção , ou seja, queremos que

nas alternativas anteriores obtivemos que

e, também que

Vamos aplicar a condição e obter os nossos pontos! Saca só!

Passo 2

Usando que , podemos expandir o produto escalar para obter

como precisamos que o resultado seja , podemos escrever

essa igualdade é verdadeira para diversos valores de , tais como

os quatro pontos podem ser escritos então como

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

Exercícios de Livros Relacionados

Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = 1 + 2 c o s θ θ = π 3

Mostre que a equação da reta tangente à parábola y 2 = 4 p x no ponto x 0 , y 0 pode ser escrita como y 0 y = 2 p ( x + x 0 ) Onde essa reta tangente intercepta o eixo x ? Use esse fato para desenhar

Encontre d y / d x e d ² y / d x ² ² ². Para quais valores de t a curva é côncava para cima? x = t - ln ⁡ t y = t + ln ⁡ t

Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes14. r = 3 - 3 c o s θ

a) Encontre a inclinação da reta tangente à trocoide x = r θ - ds e nθ , y = r - d cos ⁡ θ em termos de θ .b) Mostre que, se dr , então a trocoide não tem uma tangente vertical.