Exercícios Resolvidos de Reta Tangente e Normal a Curva

Ver Teoria

Exercício 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

Enunciado

PUCRIO - (Cálculo 2 - MAT1162) - G1 (Versão C) 2020.1

Sejam e e duas funções vetoriais. Considere a curva definida por

Encontre a função vetorial . Ou seja, calcule o produto vetorial acima.

Encontre equações paramétricas para a reta tangente à curva no ponto .

Calcule a curvatura de mesmo ponto .

Passo 1

Fala galera, tudo na paaaaz? Aqui a gente vai diretão pra questão. Afinal ela pede já na letra um produto vetorial, que pode ser definido como:

Pra achar esse produto vetorial, fazemos a determinante da seguinte matriz:

Calculando ela, temos:

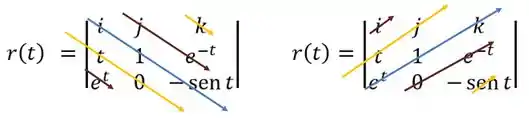
Em outras notação, isso é o mesmo que:

Passo 2

Show galera, agora vamos falar de reta tangente. Pra isso, vamos considerar que, para um parâmetro qualquer, a reta tangente a quanto é dada, de forma geral, por:

Onde:

Ponto de tangência
Vetor diretor da reta

Bem, a questão diz qual é o ponto de tangência, mas não diz qual o valor do parâmetro que resulta nesse ponto. Bora achar então:

Pra achar é bem rapidinho se igualarmos a terceira coordenada ao seu valor:

Portanto, falta agora só achar . Pra isso, a gente primeiro deriva em relação a :

E depois aplica o valor do parâmetro no ponto de tangência ():

A reta tangente então será:

Passo 3

Quase acabando povo! A última letra pede pra calcular a curvatura! É bem aplicação de fórmula mesmo. A curvatura tem essa fórmula aqui:

Vai dar um trabalho braçal fazer essas contas, então vamos com calma. Pra início de conversa, já temos . Então calcular é mole, só derivar de novo em relação a :

Como a questão ta pedindo no mesmo ponto, da letra , então na verdade o que ela quer é:

Já que achamos o valor do parâmetro . Então beleza galera! Pra começar, o denominador será:

Já o numerador, vamos achar primeiro:

De forma que o produto vetorial será:

Calculando, achamos:

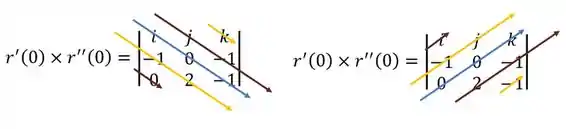
E calculando o módulo:

Ufaaa! Acabou! A curvatura será:

Resposta

Exercícios de Livros Relacionados

Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = 1 + 2 c o s θ θ = π 3

Mostre que a equação da reta tangente à parábola y 2 = 4 p x no ponto x 0 , y 0 pode ser escrita como y 0 y = 2 p ( x + x 0 ) Onde essa reta tangente intercepta o eixo x ? Use esse fato para desenhar

Encontre d y / d x e d ² y / d x ² ² ². Para quais valores de t a curva é côncava para cima? x = t - ln ⁡ t y = t + ln ⁡ t

Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes14. r = 3 - 3 c o s θ

a) Encontre a inclinação da reta tangente à trocoide x = r θ - ds e nθ , y = r - d cos ⁡ θ em termos de θ .b) Mostre que, se dr , então a trocoide não tem uma tangente vertical.