(Capítulo 13.2 – Exercício 2)
(a) Faça um esboço grande da curva descrita pela função vetorial , e desenhe os vetores e .
(b) Desenhe o vetor começando em (1, 1) e compare com o vetor
Explique porque esses vetores estão tão próximos um do outro tanto em módulo quanto em direção e sentido.
Passo 1
Oieeee galera, vamos lá ficar craques nas funções vetoriais?
a) Nesse item, queremos primeiramente desenhar a curva , descrita assim:
A curva descrita pela função vetorial dada pode ser representada pelas equações paramétricas
Da segunda equação, temos que
Enquanto na primeira equação, temos
Juntando as duas, temos que
Temos uma função quadrática de em , certo?
A curva representa uma função quadrática cuja forma é um “pedaço” de uma parábola com concavidade para a direita já que está limitado ao intervalo [0,2]. Essa aqui é a curva :
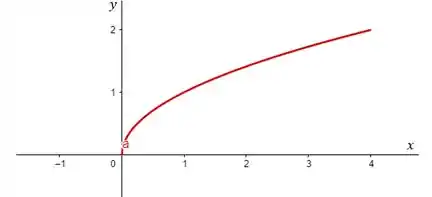
Passo 2
Showww, agora queremos encontrar os vetores e
Para encontrarmos , vamos só substituir os valores de na equação da curva, fechou?
Encontrando :
E agora encontrando :
E agora a diferença entre eles:
O gráfico abaixo mostra um esboço da curva e dos vetores de posição e , além do vetor , top?
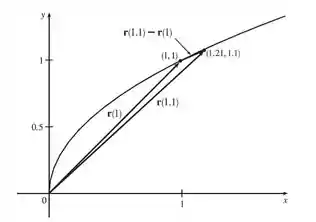
Ihuuuu, a letra a ta paga

Passo 3
b) Nesse item, queremos primeiro encontrar , ou seja, a derivada da curva aplicada em . Para obter o vetor basta derivar individualmente os componentes do vetor , igual a gente fazia lá em cálculo 1 sabe?
Assim, para , temos .
Aí, vamos comparar esse com o
Que vai ser:
Legal, vamos lá comparar esses vetores
Passo 4
No gráfico abaixo, a gente consegue ver o e o , vamos comparar
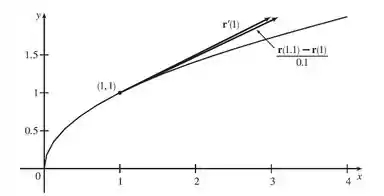
Realmente vemos que os vetores são muito próximos em módulo, direção e sentido, né???
Mas isso faz sentido! Por definição, a derivada de uma função vetorial é dada por
Para temos
Ou seja: o vetor calculado no final do passo anterior é igual à expressão dentro do limite anterior com .
Como 0,1 é próximo de 0, é toootal esperado que esses vetores sejam parecidos, sacou?
E é issoooo
Resposta
a) 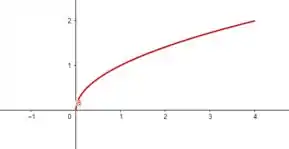
b)