Considere as duas superfícies dadas por e .
1. Esboce, separadamente, as duas superfícies, mostrando as curvas de interseção com os planos coordenados.
2. Parametrize a curva obtida pela interseção das 2 superfícies.
3. Calcule a reta tangente a no ponto .
4. Existe algum ponto de no qual a reta tangente passe na origem? Justifique.
Passo 1
1.
Vamos focar na primeira superfície, beleza?
Ela é dada por
então temos algo do tipo
portanto, essa superfície é um plano :)
Passo 2
Agora vamos ter que esboçar a figura, mostrando suas interseções com os planos coordenados. Então vamos pôr a mão na massa!
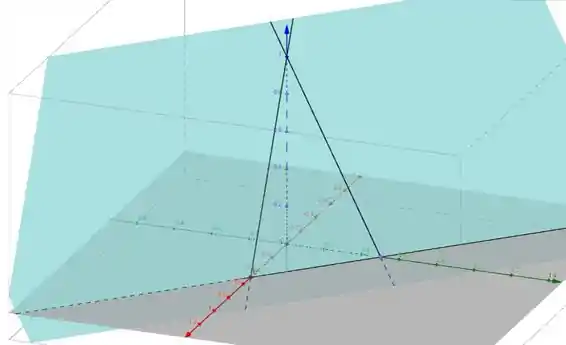
Vamos zerar uma a uma as coordenadas , e e assim determinar como o nosso plano intercepta os planos , e , respectivamente. Vamos fazer um desenho e ir completando aos poucos, beleza? Então partiu!
Fazendo vamos ter a reta
e
Então, no plano , a reta passa pelos pontos e .

Passo 3
Fazendo temos a reta
e
Ou seja, a reta passa pelos pontos e .
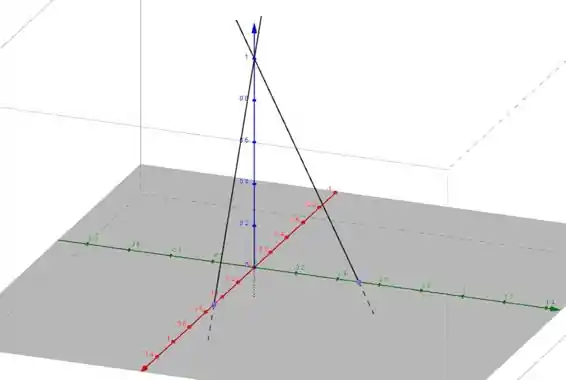
Passo 4
Fazendo temos:
e
Então a reta passa pelos pontos e . Vamos completar de novo o desenho:
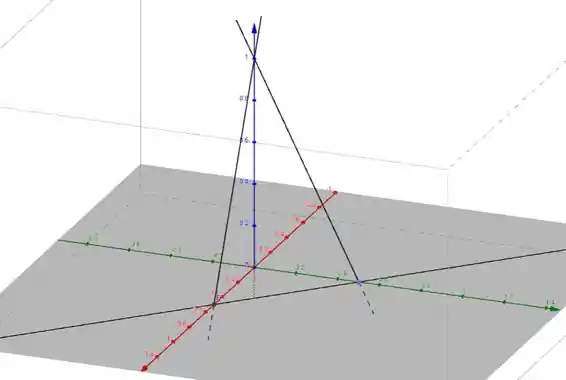
Passo 5
Então esse triângulo daí é composto pelas retas de interseção do nosso plano com os planos coordenados Ele vai ser a base do esboço do plano:
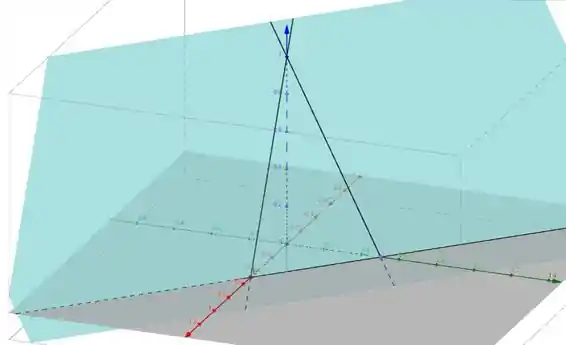
Desse ângulo dá pra ter uma visão melhor:
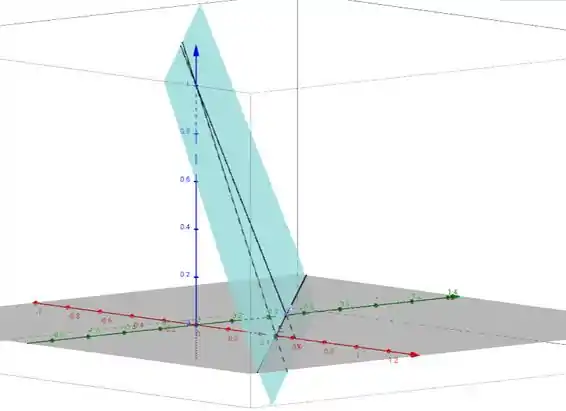
Passo 6
Ainda temos a outra superfície!
A equação dela é:
Isolando o fica:
Identificamos uma superfície do tipo
que nada mais é que a equação de um paraboloide!
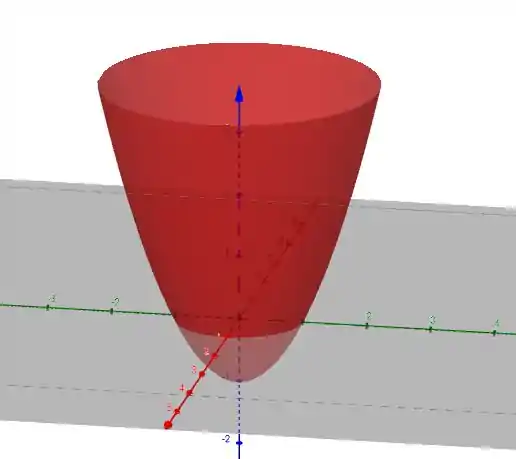
- Os dois sinais são iguais, então a superfície é um paraboloide elíptico.
- Como , vai ser mais precisamente um paraboloide circular.
- Os sinais são positivos, então ele vai ser virado pra cima.
- O valor mínimo de e é , então o mínimo absoluto e vértice do paraboloide é no ponto .
Excelente! Já da pra ter uma boa noção da figura :D
Passo 7
Agora vamos determinar as curvas de interseção do paraboloide com os planos coordenados:
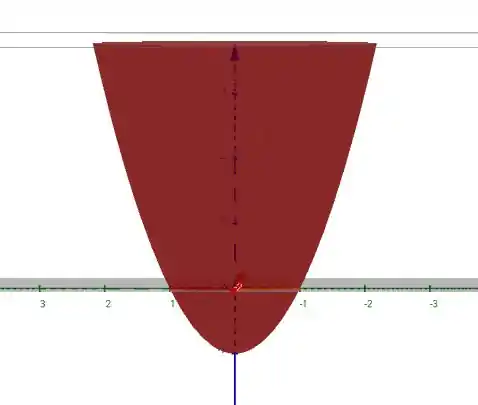
- No plano , temos
que é uma parábola voltada para cima e com mínimo em .
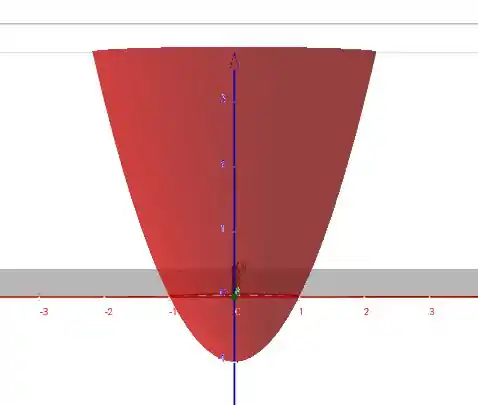
- No plano , a equação fica
que é exatamente a mesma parábola do item anterior, só passando do plano pro plano .
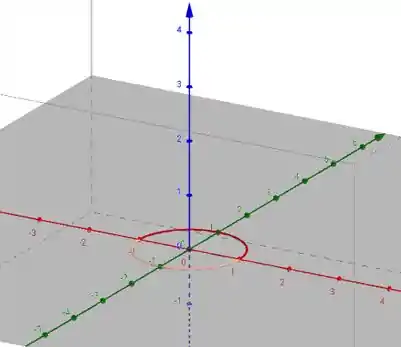
- No plano , temos
que é um círculo de raio 1 centrado em .
Passo 8
Juntando tudo, obtemos o nosso paraboloide!
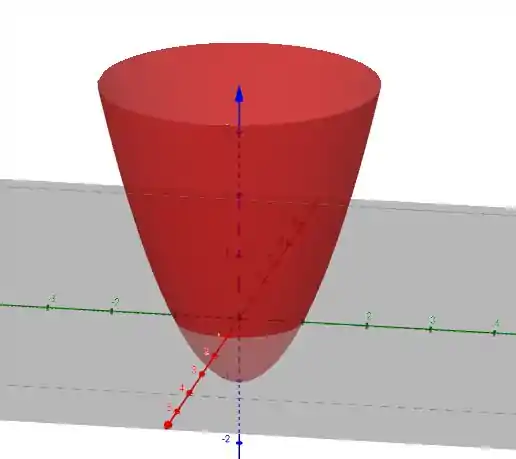
Beleza, podemos continuar!
Passo 9
2.
Agora temos que parametrizar a interseção das duas superfícies, que foi chamada de . Vamos seguir o passo a passo pra esse tipo de questão:
- Isolar uma variável de uma das equações
- Substituir na equação da outra superfície
- Parametrizar essa projeção da curva com as outras duas variáveis
- Substituir essas parametrizações na terceira variável que foi isolada
Passo 10
Na equação do paraboloide, já está isolado, então vamos usá-lo!
Substituindo na equação do plano, temos:
Completando quadrados:
E a equação de um círculo de centro e raio é:
Então a projeção de no plano é o círculo de centro e raio , tranquilo?
Passo 11
Agora temos que parametrizar essa projeção. Como é um círculo, vamos usar algo do tipo e pra gente usar e abusar da relação: .
Então vamos fazer isso:
Pra eliminarmos esse e , podemos escolher . Então vamos ter:
Para ter algo multiplicando podemos fazer . Assim:
Então, uma parametrização possível pra esse círculo é:
Passo 12
Show! Agora só falta substituir essa parametrização na variável :
Logo, uma parametrização de é:
Passo 13
3.
Agora queremos a reta tangente a no ponto . Beleza, precisamos descobrir em que temos :
O que nos dá um sistema:
Pela primeira equação:
Como :
Se quiser, você pode verificar que as outras equações são respeitadas :)
Passo 14
Pra achar a reta tangente em , vamos precisar de . Então vamos começar calculando :
Então em temos:
Logo, uma parametrização da reta tangente a em é:
Passo 15
4.
Enfim, pra finalizar essa pergunta gigante, ele nos pergunta se existe um ponto de onde a reta tangente passa na origem.
Na verdade, vai ser até simples de responder.
Vejamos, por definição a curva está contida no plano . Então qualquer reta tangente a um ponto de deve estar contida no plano! Ele é 2D, a reta tangente não pode simplesmente sair por aí!
E como a origem não está no plano, nenhuma reta tangente de pode passar nela!
Então é isso, fechamos a questão! (Aleluia!!)
Resposta
1.
2.
3.
4.
Não.