5) Calcule o volume do sólido obtido pela rotação ao redor do eixo da área finita delimitada pelas curvas e
Passo 1
A primeira coisa a fazer é pensar assim: o sóldio que queremos calcular o volume é um sólido de revolução. Se é um sólido de revolução, vai ser importante a gente entender a aparência da área revolucionada. E que melhor forma de fazer isso do que vendo as curvas?
Se elas juntas fecham uma região, então bora ver em que valores de elas se encontram pra fechar essa região:
Elevando as duas ao quadrado, temos:
Vamos ter então que:
Já sabemos então que a região está delimitada entre:
Que vão ser exatamente os limites de integração
Passo 2
Agora, bora escolher um método de integração pro calculo desse volume. O método das cascas cilíndricas já dá pra gente uma fórmula pronta pra rotação ao redor do eixo . Vamos ter então:
Como nossas duas funções são positivas no intervalo de integração e nem precisamos nos preocupar com sinais. Mas que função a gente põe dentro da integral? Pra sacar isso, dá uma olhada no gráfico da região a ser revolucionada:
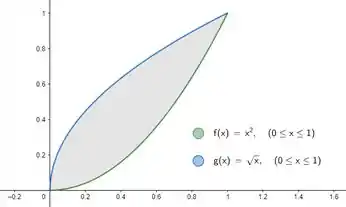
E veja! Temos uma função que está sempre em cima da outra nos intervalos de integração! Pra saber qual sem precisar do esboço, basta a gente fazer um teste de sinais. Saca só esse exemplo:
Usando esse valor de na equação das curvas:
Opa, então no intervalo de integração, vamos ter
Mas ainda não acabou. Afinal, temos duas curvas e só um na fórmula. Veja bem, se fosse , íamos ter a seguinte região rotacionada ao redor do eixo :
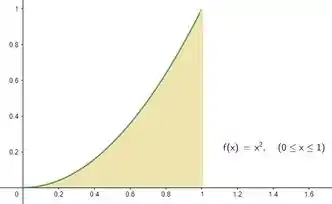
E se escolhêssemos pra ser , íamos ter a seguinte região:
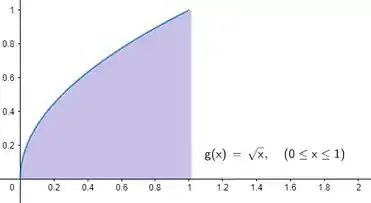
Saca só: a região roxa é maior que a região bege. Então se calcularmos o volume dessas regiões, o volume da região roxa rotacionada será maior que a da região bege rotacionada. Sendo assim, se eu escolher:
Vai ser como se estivéssemos calculando o volume roxo menos o volume bege que, no final das contas, é o volume cinza que a gente quer mesmo:
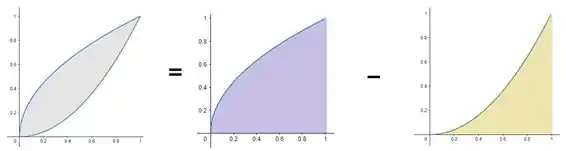
Passo 3
Vamos fechar então a questão calculando a integral. Do método escolhido:
Seja:
Vamos ter: