Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cascas Cilíndricas

Ver Teoria
Exercício 291234567891011121314151617181920212223242526272830313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere a região plana R definida por

R = x ,   y ∈ R |   x ≤ 4 ,   - ln ⁡ x - 1 ≤ y ≤ 0

Seja S o sólido de revolução obtido pela rotação de R em torno do eixo y .

Letra b) Calcule o volume de S pelo método que preferir.

Passo 1

Letra b) Como vamos girar

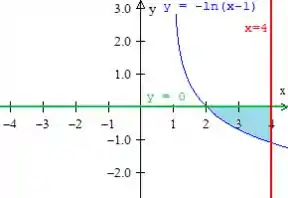
Ao redor de y , é super aconselhável calcular o volume pelo método das cascas! Bora?

Aplicando a fórmula do cálculo de volume pelas cascas cilíndricas, ou seja:

V o l S = ∫ a b 2 π x g x - h x d x

Agora, quem é g ( x ) e h ( x ) no nosso caso?

Bem, a g ( x ) deve ser a função que está por cima. No caso, quando giramos a nossa região R ao redor de y , notamos que a função que fica por cima é g x = 0 .

Quanto a h ( x ) , a função que está por baixo é o ln ⁡ ,   logo h x = - ln ⁡ ( x - 1 )

V o l S = ∫ a b 2 π x 0 - ( - ln ⁡ ( x - 1 ) d x

V o l S = ∫ a b 2 π x ( ln ⁡ ( x - 1 ) ) d x

Onde a e b são os termos de variação de x dentro da região R , ou seja, ele está indo de a = 2 e b = 4

V o l S = ∫ 2 4 2 π x ( ln ⁡ ( x - 1 ) ) d x

Basta resolver essa integral aí e correr para o abraço!:)

Passo 2

2 π é uma constante, podendo cair fora da integral

V o l S = 2 π ∫ 2 4 x ( ln ⁡ ( x - 1 ) ) d x

Para resolver essa integral aí, vamos calcular a integral indefinida primeiro nos preocupando com esses limites depois (para facilitar nas contas rs) !

Observe que a derivada do ln ⁡ é uma coisa mais simples, o que nos sugere uma integração por partes:

u = ln ⁡ ( x - 1 )       →             d u = 1 x - 1 d x

d v = x d x           →                     v = x 2 2

Pela fórmula

∫ u d v = u v - ∫ v d u

teremos

∫     x ( ln ⁡ ( x - 1 ) ) d x = x 2 2 ln ⁡ ( x - 1 ) - 1 2 ∫ x 2 x - 1 d x

Passo 3

Ganhamos outra integral ∫ x 2 x - 1 d x que a gente pode resolver fazendo uma pequena manipulaçãozinha:

Vamos diminuir 1 em cima e ao mesmo tempo somar com 1 para não alterar o resultado:

∫ x 2 x - 1 d x = ∫ ( x 2 - 1 ) + 1 x - 1 d x

Por que fazer isso é interessante? Porque aí a gente pode separar x 2 - 1 naquele produto notável x 2 - 1 = ( x - 1 ) ( x + 1 ) , se lembra?

∫ ( x 2 - 1 ) + 1 x - 1 d x = ∫ ( x 2 - 1 ) x - 1 + 1 x - 1 d x

∫ ( x - 1 ) ( x + 1 ) x - 1 + 1 x - 1 d x

Cortando esse cara de cima com o de baixo da primeira parcela, ficamos

∫ x + 1 + 1 x - 1 d x

Resolvendo essa integral integrando termo a termo:

∫ x + 1 + 1 x - 1 d x = x 2 2 + x + ln ⁡ ( x - 1 )

Passo 4

Retornado para a integral definida

∫ 2 4 x ( ln ⁡ ( x - 1 ) ) d x = x 2 2 ln ⁡ x - 1 - 1 2 ∫ x 2 x - 1 d x 2 4

∫ 2   4   x ( ln ⁡ ( x - 1 ) ) d x = x 2 2 ln ⁡ x - 1 - 1 2 x 2 2 + x + ln ⁡ ( x - 1 ) 2 4

Substituindo os limites

4 2 2 ln ⁡ 4 - 1 - 4 2 4 + 4 2 + ln ⁡ 4 - 1 2 - 2 2 2 ln ⁡ 2 - 1 - 2 2 4 + 2 2 + ln ⁡ 2 - 1 2

Simplificando as continhas lembrando que ln ⁡ 1 = 0

∫ 2   4   x ( ln ⁡ ( x - 1 ) ) d x = 15 2 ln ⁡ 3 - 4

Portanto o volume será:

V o l S = 2 π ∫ 2   4   x ( ln ⁡ ( x - 1 ) ) d x =

15 π ln ⁡ ( 3 ) - 8 π

Resposta

V o l S = 15 π ln ⁡ ( 3 ) - 8 π

Exercícios de Livros Relacionados

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em