Considere a região delimitada pelo gráfico da função e pelo eixo , com .
Calcule o volume do sólido de revolução obtido pela rotação dessa região em torno do eixo .
Passo 1
Vamos começar visualizando essa região.
A função é bem simples, então podemos esboçar o gráfico dela:
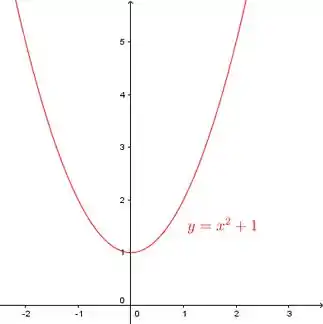
Mais especificamente, no intervalo , que foi o intervalo pedido:
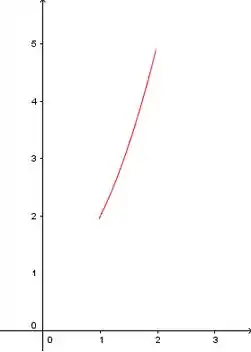
Então a região que o enunciado falou é:
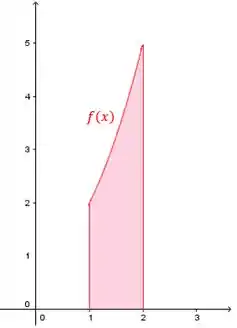
Passo 2
Aplicando a fórmula, o volume do sólido de revolução é
Passo 3
Agora é só desenvolver isso e integrar!