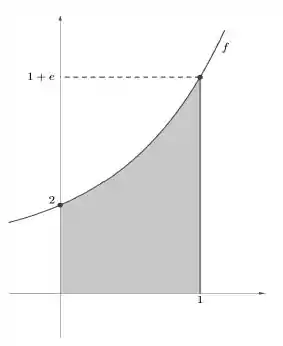
Considere a região plana definida por:
Seja o sólido de revolução obtido pela rotação de em torno do eixo
- Esboce abaixo a região plana
- Utilizando o Método dos Discos, determine uma soma de duas integrais que forneça o volume de . Obs: Nesse item não é necessário calcular a integral
- Utilizando o Método de Cascas, determine uma integral que forneça o volume de . Obs: Nesse item não é necessário calcular a integral
- Calcule o volume de pelo método que preferir
Passo 1
Fala povo, tudo certo? Vamos começar esboçando essa região porque isso vai ajudar muito a gente. Pra começar, note que está delimitado entre o eixo e uma curva, essa curva sendo:
Pelas propriedades das exponenciais, a gente tira uma informação impostantíssima que auda a gente no esboço:
Mas como , só vamos precisar nos preocupar com a parcela de que está no primeiro quadrante e que sai de um ponto pertencente ao eixo . Que ponto é esse? Oras, basta fazer:
Agora, como , é interessante a gente saber também em que ponto essa exponencial para. Pra isso basta a gente fazer:
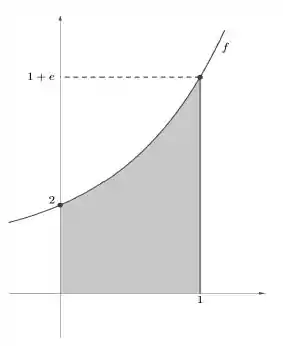
Beleeeza, como a região é a área abaixo da curva e sabemos onde a curva começa e onde ela termina, temos o suficiente pra esboçar:
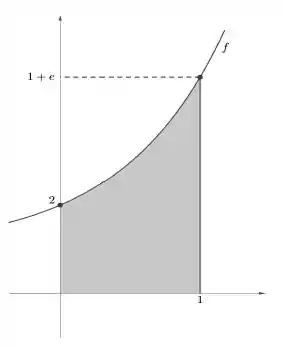
Passo 2
Essa aqui é pegadinha em! Vamos tomar cuidado. O método dos discos sempre vale pra rotação em torno do eixo horizontal. Só que, por padrão, sempre colocamos o eixo como o horizontal. Então pra rodar em torno do eixo maaaas usar esse método, o que temos que fazer com o gráfico são duas operações:
![]()
Dessa forma os eixos trocam de lugar e podemos usar o método. A região vai ficar:
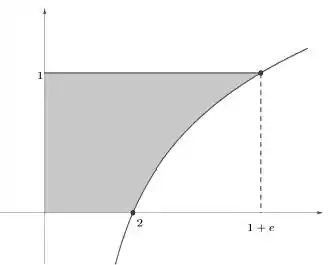
Agora sim podemos usar o método e integrar em função de . Só temos que nos atentar ao fato de que essa mudança acaba invertendo função. Essa curva, , terá a seguinte lei de formação:
Agora sim temos tudo que precisamos. Entendendo a região acima como a região da esquerda menos a da direita, calculamos o volume pelo Método dos Discos usando, pra esquerda, função constante e a pra direita a própria curva . O volume do sólido de revolução seria também uma subtração e escreveríamos como:
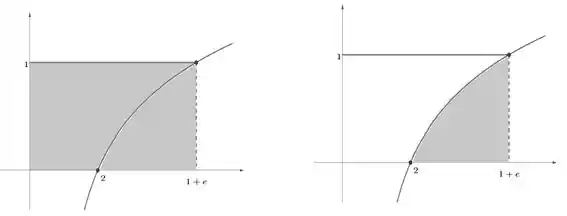
Passo 3
Pro Método das Cascas a gente pode dar uma relaxada porque ele já é bem direto ao ponto. Como ele é tradicionalmente usado para rotações ao redor do eixo vertical e em:
O eixo vertical já é o eixo , só precisamos mesmo aplicar o método! Uma única integral nos salva! O volume será:
E como essa integral é mais simples a gente já aproveita e calcula logo o volume
A primeira integral fica:
Pra integral que sobrou, vamos ter que fazer uma integração por partes já que temos um polinômio vezes uma exponencial, seja, pela regrinha do LIATE:
A integração por partes fica
E aplicando os limites de integração:
O volume final será: