Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo x:
Passo 1
Saaalve galerinha, animam destruir essa questão comigo?
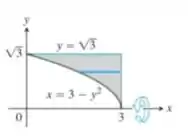
O enunciado nos diz que há uma região criada pelo limite das seguintes retas:
A dúvida é: quando essa região rotacionar ao redor do eixo x, qual vai ser o volume do sólido? Vem descobri comigooo!
Passo 2
A ideia aqui é usar o método da casca que tem o objetivo de calcular o volume de uma região segundo a fórmula:
O raio da casca vai ser a variação no eixo y, então , pois a rotação é no eixo x.
E a altura da casca é a curva .
Substituindo na fórmula da casca, temos:
Passo 3
E o nosso último passo vai ser resolver essa integral LINDA!
Fazendo uma simplificação para facilitar resolver a integral:
Integrando, teremos:
Resolvendo primeiro os termos no parêntese:
Prontinho, encontramos o volume total uhhhh!
Curtiu a resolução? Responde Aí!!