UFABC – Sem Campus – Funções de Uma Variável – Listas – Listas FUV – GRADMAT – Lista 11 – Integrais Impróprias – Questão 3 – Alternativa a)
Use o método das cascas cilíndricas para calcular o volume do sólido obtido rotacionando a região em torno do eixo . Esboce o sólido obtido.
a) é limitada por baixo pelo eixo e acima por entre .
Passo 1
Opa, tudo certinho?
Já de cara, vamos dar uma olhada em quem é a região que vamos rotacionar, beleza? Temos o seguinte:
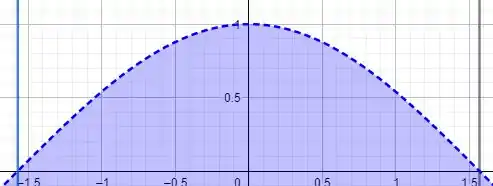
Ao rotacionar esta região em torno do eixo-y, obtemos algo do tipo:
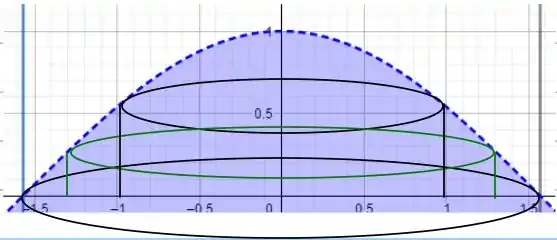
Imagine como uma calota. Os cilindros preto e verde, estão aqui para exemplificar o método que iremos utilizar. Para calcularmos qual é o volume deste sólido devemos somar o volume de diversas cascas cilíndricas de raio e altura , de forma que:
Então, bora lá!!
Passo 2
Com o método calcula tendo como base o raio das cascas cilíndricas, nós iremos utilizar limites de integração que vão de à , obtendo:
Esta integral deve ser resolvida por partes! Bora lá!
Passo 3
Se lembrar do método do LIPTE (Logaritmo, Inversa, Polinomial, Trigonométrica e Exponencial) que te dá a ordem para escolher quem é o seu na integral por partes, verá que é conveniente fazer a escolha:
E
De forma que possamos escrever nossa integral como:
Agora está mais de boinhas neh? Bora continuar!
Passo 4
Temos que esta integral já está em um formato que vale a pena saber de cor! Temos que:
Portanto:
Vamos voltar a nossa integral original!
Passo 5
Temos então para o nosso volume que:
Essa alternativa foi isso! Te vejo na próxima! Até já!