UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 3.4a
(4) Utilize o Teorema de Pappus-Guldin para determinar:
(a) o volume do sólido de revolução gerado pela rotação do hexágono regular inscrito no círculo ao redor do eixo .
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema temos que aplicar o teorema de Pappus-Guldin para determinar o volume do solido de revolução gerado pela rotação, através do eixo , do hexágono regular inscrito no círculo dado pela equação .
Tem ideia de como fazer isso? 🤔
O teorema de Pappus-Guldin nos diz que o volume de um solido de revolução é dado por
Onde é a distância do centroide da área a ser revolucionada e é sua área.
Primeiramente vamos obter o gráfico da área que vamos revolucionar, calcular sua área e a distância do seu centroide até o eixo de rotação.
Sacou? Bora começar! 😉
Passo 2
Esboçando a circunferência com o hexágono inscrito temos...
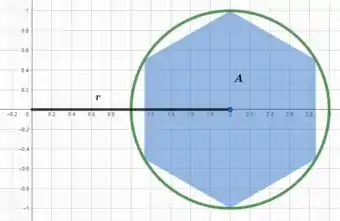
Perceba que o centroide do hexágono e o centroide do círculo são os mesmos, portanto podemos calcular como
Já pode ser calculado a partir da equação
Como nosso hexágono é regular, então é igual ao raio da circunferência, ou seja
Portanto...
Tranquilo até aqui? 😉
Passo 3
Substituindo e na fórmula do teorema, temos
É isso! Essa resolução te ajudou? Responde Aí! ✌
