UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 10a
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
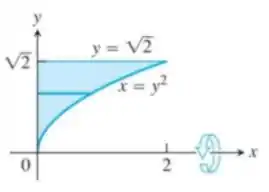
Passo 1
Eai galerinhaaa, tudo bem com vocês?
Nessa questão temos uma região no plano , e rotacionamos ela em torno do eixo . A região rotacionada é a região entre as curvas:
Ou seja, é a região representada na figura abaixo:
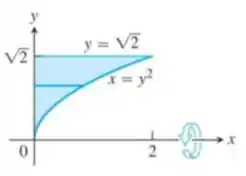
O enunciado nos pede para calcular esse volume utilizando o método da casca.
Puts, mas só tô acostumado a usar o método da casca quando é rotação em torno do eixo , que fica:
Caaalma galera!! Só precisamos fazer alguns ajustes. Já que agora a rotação é em torno do eixo , onde na nossa expressão anterior tínhamos vamos trocar por . Assim, ficamos com:
Esse é o volume obtido pela rotação, em torno do eixo , da região entre a curva e o eixo . Sacaram?
Ufaa!
Vamos então montar a integral para a nossa curva e calcular o volume 😊
Passo 2
Como comentamos no passo , a nossa região está limitada entre as curvas:
Mas isso é se a gente pensar nas funções que delimitam a região na direção do eixo (ou seja, por cima e por baixo). Como aqui a gente inverteu, vamos ter que pensar em quem delimita a nossa região pela direita e pela esquerda?
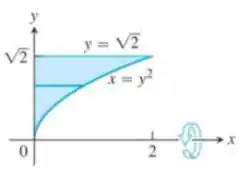
De fato, ela é a região entre a curva e o eixo .
No intervalo de:
Assim, como pelo método das cascas:
Teremos:
Colocando as constantes para fora:
Usando que:
Vem:
Portanto:
Prontinhoo!! Matamos mais uma questão, espero que vocês tenham gostado 😊