UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 9c
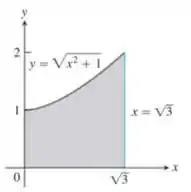
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
Passo 1
Opa pessoal, quem tá animado pra matar mais uma questãooo?! Vem junto com a gente 😊
Precisamos calcular o volume do sólido obtido quando rotacionamos a região:
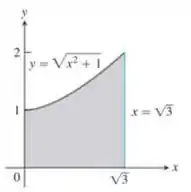
em torno do eixo . E, o enunciado pede para fazermos isso utilizando o método da casca. Vocês lembram dele?
Ele fala que se rotacionarmos uma região abaixo da curva em torno do eixo , o volume do sólido obtido vale:
Perfeito! Agora que já sabemos disso, vamos montar a integral e depois calcular o seu resultado!
Passo 2
Pra montar a integral que representa o nosso volume , precisamos analisar melhor a região que será rotacionada:
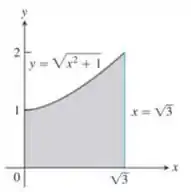
Nota que ela é a região abaixo da curva:
E, além disso, está no intervalo:
Assim, como o nosso volume , pelo método das cascas, vale:
Para a nossa região, vamos ter:
Excelente!
Passo 3
Por fim, vamos calcular a nossa integral.
Colocando as constantes para fora da integral:
Pra calcular essa integral, é bem útil fazermos uma mudança de variáveis. Chamando:
Além disso, quando :
Quando :
Substituindo na integral:
Usando que:
Temos:
Logo: