4. Encontre o valor da área delimitada pelo gráfico da função , o eixo e as retas verticais e .
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que calcular a área delimitada por região!
Para fazermos esse calculo vamos aplicar a seguinte fórmula:
Onde é a região que vamos calcular a área e os limites de integração.
Então agora nós temos que encontrar quem é essa função que vamos integrar e quem são os limites de integração.
Agora lá!
Passo 2
Vamos começar achando os limites de integração! Para isso, vamos traçar todas as linhas que delimitam a nossa região em um gráfico.
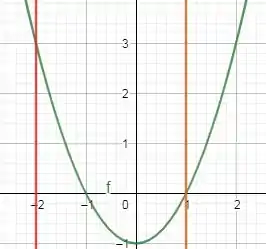
Onde a reta verde representa o gráfico ; e as linhas vermelha e laranja são as retas verticais e , respectivamente.
Repara que temos uma região que está acima do eixo , entre e . E outra área que está abaixo do eixo , entre e .
Sendo assim, vamos ter que calcular a área das duas regiões em separada e soma-las.
Agora bora montar a nossa integral!
Passo 3
Passando tudo para a fórmula do volume, ficamos com
Repara que o sinal da função da segunda área está negativo, pois estamos integrando abaixo do eixo . Além disso, como a região é simétrica de na segunda integral, podemos integrá-la de até e depois dobrar esse valor.
Resolvendo a integral indefinda, aplicando a regra do polinômio para cada termo,
Ficamos com
Agora vamos aplicar os limites de integração!
Passo 4
Tinhamos,
Logo,