UFCG - Sem Campus - Cálculo Diferencial e Integral II- Listas - Teste 9 - Lista 3 - Questão 13 - Alternativa b)
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação da região sombreada em torno do eixo indicado:
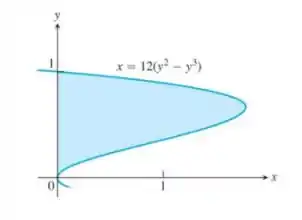
reta
Passo 1
Opa! Tudo bem com você?
É pedido para que calculemos o volume do sólido de revolução obtido quando se rotaciona a região dada acima
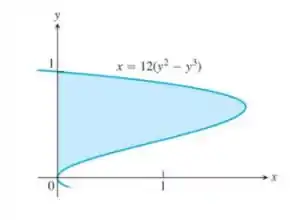
ao redor da reta . O sólido de revolução obtido é
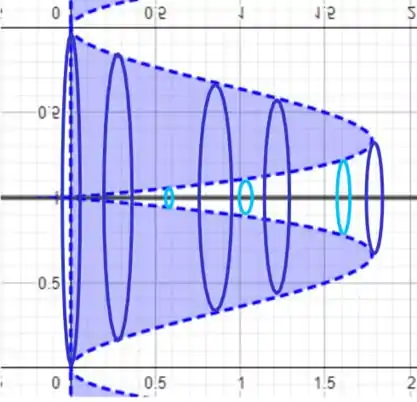
É um montinho com um buraco no seu topo, como aqueles bolos vulcão! Consegue visualizar? O enunciado pede para que usemos o método das cascas (ou método das cascas cilíndricas) para resolver este problema! Este método se trata de somar infinitamente diversas cascas cilíndricas de espessura , altura dada como , e em nosso caso, temos que o raio pode ser obtido como , devido a nossa escolha de referencial, portanto, temos que o volume é calculado como
Vamos usar essas informações para calcular o nosso volume! Vem comigo!
Passo 2
Como estamos integrando em a nossa região delimitada pelos valores de e , em que a função cruza o eixo , temos então que utilizando a função , e colocando os limites adequados, obtemos que
Precisamos distribuir os produtos e resolver as integrais, nós temos que
Podemos juntar as duas integrais que são iguais e obter
Para resolver estas integrações é preciso identificar as primitivas utilizando a seguinte regrinha
Vamos aplicar isso no próximo passo! Bora lá!
Passo 3
Usando a regrinha que apresentei para , temos que
Ou simplesmente
Analogamente, para , temos que
e, para , temos que
Usando estes resultados em nosso volume, temos então que
Temos então a seguinte soma de termos
Ou seja, nosso volume é simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!