UFRJ – Cálculo 1 – 2020.2 – P4 – Exercício 7
Seja o sólido obtido pela rotação da região delimitada pelas curvas e em torno da reta . Qual é o volume desse sólido?
a)
b)
c)
d)
e)
Passo 1
Fala galerinha, beleza?
Queremos achar o volume do sólido obtido pela rotação da região delimitada pelas curvas e em torno da reta . A seguir, desenhamos as curvas e a reta :
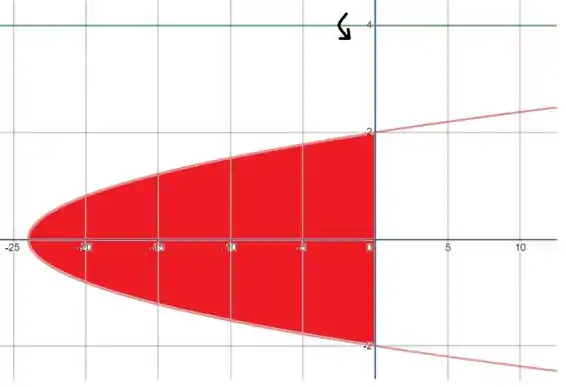
A região limitada pelas curvas está pintada em vermelho. A reta está em verde. Olhando para a expressão , vemos que se trata de uma parábola “deitada” com vértice no ponto . Além disso, a intersecção com a reta ocorre nos pontos com .
Passo 2
Para calcular o volume do sólido, usamos o método das cascas cilíndricas:
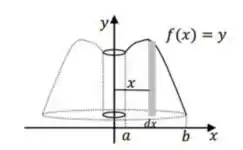
No caso do desenho acima, o volume é dado por
Podemos interpretar essa integral como sendo
Na situação do problema que queremos resolver, a rotação é feita em torno de uma reta paralela ao eixo horizontal, de modo que a integral deve ser feita na variável :
Passo 3
Pegando uma casquinha cilíndrica horizontal, temos que
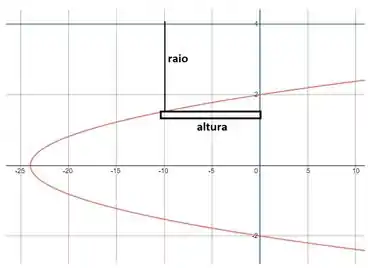
O raio é dado por
Já a altura é
Como estamos olhando na região , temos que
Assim, o volume é dado por
Ou ainda, invertendo a ordem nos dois parêntesis:
A resposta está na alternativa C 😉.
Resposta
Alternativa C.