UFCG - Sem Campus - Cálculo Diferencial e Integral II- Listas - Teste 9 - Lista 3 - Questão 14 - Alternativa b)
Calcule o volume do sólido obtido com a rotação da região triangular limitada pelas retas , e , em torno:
do eixo , usando o método da casca.
Passo 1
Opa! Tudo bem com você?
O enunciado pede para que calculemos o volume do sólido de revolução da região delimitada pelas retas
, e
Esta região é a seguinte
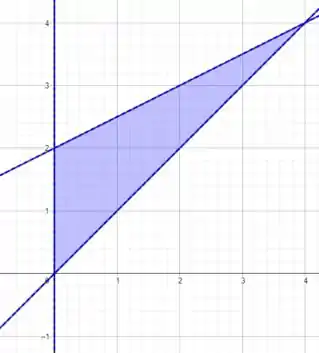
A reta superior é e intercepta o eixo em . A reta inferior é e cruza o eixo em . A intersecção entre as duas acontece em . Nesta alternativa precisamos realizar a revolução em torno do eixo , de forma que obtemos o seguinte sólido de revolução
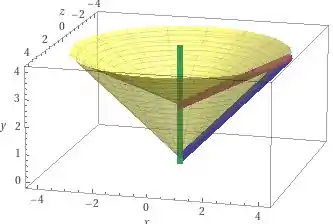
A linha vermelha é a reta , a linha azul a reta , e reta verde indica o eixo . O enunciado nos pede para utilizarmos o método das cascas! Vamos relembrá-lo rapidamente!
Passo 2
O método das cascas pode ser resolvido calculando o volume de uma casca cilíndrica de espessura , altura e circunferência , ou seja, temos
O raio em nosso caso é simplesmente , no entanto, a altura será a diferença entre a função superior, e a inferior, ou seja, temos que
O volume é então calculado através de
Agora é só resolver as integrais! Bora lá?
Passo 3
Aqui precisamos identificar primitivas da forma
Temos que com
e, para , temos
Com estes resultados em mãos podemos escrever que
Ou, simplesmente
A questão foi isso! te vejo na próxima! Tchauzinho!