UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 3.4c
(4) Utilize o Teorema de Pappus-Guldin para determinar:
(c) o centroide da região .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos que aplicar o teorema de Pappus-Guldin para determinar o centroide da área do solido de revolução gerado pela rotação, através do eixo , da região .
Tem ideia de como fazer isso? 🤔
O teorema de Pappus-Guldin nos diz que o volume de um solido de revolução é dado por
Onde é a distância do centroide da área a ser revolucionada e é sua área.
Primeiramente vamos obter o gráfico da área que vamos revolucionar, calcular sua área e a distância do seu centroide até o eixo de rotação.
Sacou? Bora começar! 😉
Passo 2
Vamos começar esboçando a região ...
Essa região se trata da região formada pelo setor circular dado pela inequação em que e .
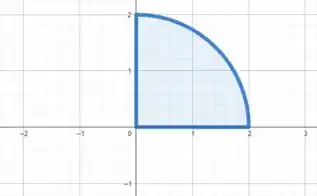
Essa região se trata de de uma circunferência, portanto podemos calcular sua área como
No caso, como podemos obter da equação do círculo.
Perceba que ao rotacionar essa área, vamos obter uma semiesfera de raio , portanto o volume do objeto pode ser obtido como
Tranquilo até aqui? 😉
Passo 3
Vamos substituir as informações que encontramos até aqui na equação do teorema
Simplificando e isolando
Perceba que no eixo e no eixo há uma simetria na região, logo o centroide da região terá as mesmas coordenadas em e
Fim! Iae, o que achou? Responde Aí! 😁
