UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 9a
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
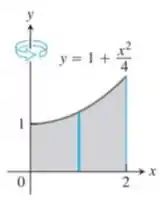
Passo 1
Oi oi oi gente do bem, como vocês estão?
Nessa auspiciosa questão haha, precisamos usar o método da casca para determinar o volume do sólido obtido quando rotacionamos, em torno do eixo a região:
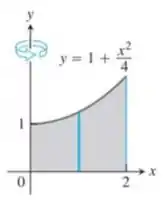
Ou seja, a região abaixo da curva:
quando .
Mas, vocês lembram o que diz o método da casca?
Bom, basicamente ele diz que se rotacionarmos uma região abaixo da curva em torno do eixo , o volume do sólido obtido vale:
Boaaa! Agora que já revisamos o método, é só montarmos a integral e resolvê-la.
Passo 2
Como comentamos anteriormente, nossa região está abaixo de , e está no intervalo .
Já que:
Teremos:
Colocando as constantes para fora da integral, temos:
Usando que:
Vem que:
Terminamosss! Conseguiu entender a solução? Responde aí!