Cálculo de Volumes através de Integrais
Seja . Determine o volume do sólido obtido pela rotação de em torno do eixo .
Passo 1
Primeiro desenhamos a região, levando em conta que é uma parábola de uma só raiz em , concavidade para cima, e que toca o eixo em:
A região será:
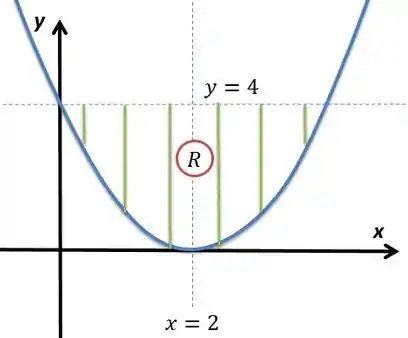
Passo 2
A gente pode, fazer essa integral então pelo método das cascas cilíndricas, reparando que um cilindro com eixo em teria raio valendo o próprio e altura indo do limite superior de até o inferior, ou seja, . Os limites de integração seriam as interseções que já achamos. Assim, nossa integral teria essa cara:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em