Cálculo de Volume através de Integrais
Encontre o volume obtido pela rotação da placa limitada por , , e , em torno do eixo , sendo .
Passo 1
O cara quer o que nós calculemos o valor do volume rotacionado em torno de da região dada por:
Com e .
Vamos, em primeiro lugar, desenhar . Eu não sei com exatidão como se comportaria o num gráfico, mas deve ser algo parecido com uma cossenóide.
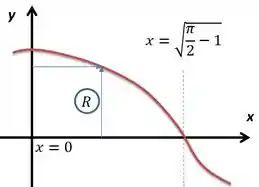
Ali eu representei também duas setas, uma horizontal e outra vertical. A horizontal vai medir em relação ao eixo o raio de rotação de em relação ao mesmo eixo. Já a seta vertical medirá uma distância do gráfico até o eixo . Enfim, como a rotação é em torno do eixo , podemos constatar que a reta horizontal medirá o raio dessa rotação e a vertical a altura. Fazendo o volume por cascas cilíndricas teríamos:
Passo 2
Vamos resolver a integral com uma substituição:
Esse é nosso volume!