UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 2.4a
Utilize o método da casca cilíndrica para determinar o volume do sólido gerado pela rotação da região limitada por:
, em torno do eixo y.
Passo 1
Eaew, belezinha?
Temos que encontrar o volume do sólido de rotação ao girarmos em torno do eixo y a região . Foi pedido para utilizarmos o método das cascas cilíndricas, sendo esse método aplicado quanto temos retângulos, de largura infinitesimal, paralelos ao eixo de rotação. Então o volume total é dado pela soma dos volumes das cascas cilíndricas formadas quando esses retângulos são rotacionados ao redor do eixo. No caso, a região a ser rotacionada em torno do eixo y é apresentada no gráfico abaixo:
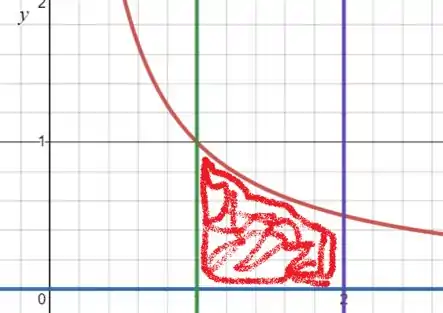
sendo:
o raio do cilindro formado;
a altura do cilindro;
a largura da casca.
Então o volume total fica:
Então vamos lá resolver essa integral!
Passo 2
Temos que resolver a integral
Então, resolvendo a integral e aplicando os limites
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
;