Fixado considere a região delimitada pelas curvas e . Considere também o sólido dado pela rotação de em torno do eixo . Se é a área de e é o volume de , então:
- não depende de e é diretamente proporcional a
- é diretamente proporcional a e é diretamente proporcional a
- é diretamente proporcional a e é diretamente proporcional a
- e são diretamente proporcionais a
- e são diretamente proporcionais a
Passo 1
Vamos começar visualizando o problema com um esboço:
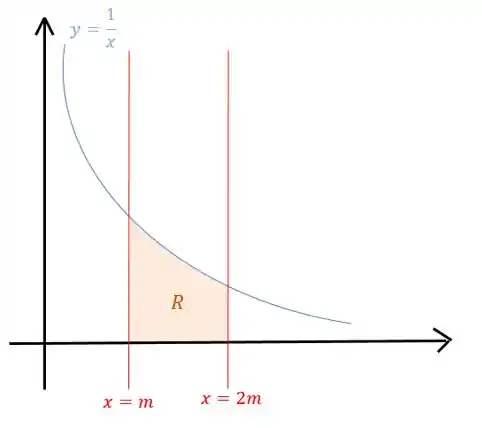
Passo 2
Vamos começar pela área . Ela vai ser dada por:
O que vai dar:
Pelas propriedades do logaritmo:
Então não depende de , e isso já nos basta pra dizer que a alternativa certa é a letra (a)!
Aliás, muito loko né, não importa que você escolher a integral vai dar sempre .
Passo 3
Mas bom, a alternativa (a) também diz que é diretamente proporcional a , então vamos testar isso.
Pelo método das cascas cilíndricas:
Ótimo, o vai cortar:
Então de fato constatamos que é diretamente proporcional a . A letra (a) está mesmo certa!
Resposta
Letra (a)