Cálculo de Volumes através de Integrais
Seja a região compreendida entre os gráficos de e para , como mostra a figura abaixo:
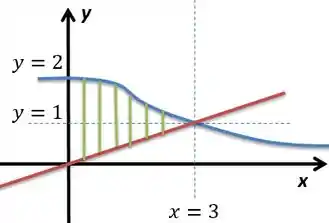
Calcule o volume do sólido obtido pela rotação de em torno de .
Calcule o volume do sólido obtido pela rotação de em torno de .
Passo 1
Não precisamos nem nos concentrar no desenho, nas interseções, nos limites de integração, já está tudo lá. A questão toda é aplicar a fórmula da melhor maneira possível.
Ok, na letra queremos girar a região em torno do eixo . O gráfico azul está mais distante do eixo , a reta vermelha está mais próxima. Assim, o volume que nos interessa seria a diferença do volume feito para o gráfico azul e o gráfico vermelho, tudo por sessões transversais (já que giramos em torno do eixo ):
Os limites, como já esclarece o enunciado, são e . Ficamos com , :
Passo 2
Vamos resolver essa primeira integral por substituição trigonométrica (repara que o denominador cai no caso da substituição de por :
Devemos mudar os limites também, superior e inferior:
Como temos a relação trigonométrica que diz que , podemos substituir na integral ficando da seguinte maneira:
Passo 3
Agora falta fazer a subtração com o outro termo da integral:
Assim, o volume total é:
Passo 4
Agora giramos em torno do eixo . Vou tentar a integral por cascas cilíndricas, para não ter o trabalho de ter que inverter as funções e os limites de integração. Se fizermos assim, nós ficaremos com o volume sendo a rotação do gráfico azul menos a do gráfico vermelho em torno do eixo :
Os limites de integração são os mesmos, assim como as funções:
O primeiro termo da integral pode sofrer a seguinte substituição para ser resolvido:
Passo 5
Assim, sendo a outra integral a de um polinômio normal, ficamos assim: